Bài 27 trang 205 SGK giải tích 12 nâng cao

Hãy tìm dạng lượng giác của các số phức: \(\overline z \,;\, - z;\,{1 \over {\overline z }};\,kz\,\left( {k \in \mathbb R^*} \right)\) trong mỗi trường hợp sau:

\(a)\,z = r\left( {\cos \varphi  + i\sin\varphi } \right)\,\left( {r > 0} \right);\)                               

\(b)\,z = 1 + \sqrt 3 i.\)

Giải

\(\eqalign{  & a)\,\overline z  = r\left( {\cos \varphi  - i\sin \varphi } \right) \cr&= r\left( {\cos \left( { - \varphi } \right) + i\sin \left( { - \varphi } \right)} \right)  \cr  &  - z =  - r\left( {\cos \varphi  + i\sin \varphi } \right) \cr&= r\left( {\cos \left( {\pi  + \varphi } \right) + i\sin \left( {\pi  + \varphi } \right)} \right)  \cr  & {1 \over z} = {z \over {\overline z .z}} = {1 \over r}\left( {\cos \varphi  + i\sin \varphi } \right)  \cr  & k.z = kr\left( {\cos \varphi  + i\sin \varphi } \right)\,\,\text{nếu}\,k > 0  \cr  & kz =  - kr\left( {\cos \left( {\pi  + \varphi } \right) + i\sin \left( {\pi  + \varphi } \right)} \right)\,\,\text{nếu}\,\,k < 0 \cr} \)

\(b)\,z = 1 + \sqrt 3 i = 2\left( {{1 \over 2} + {{\sqrt 3 } \over 2}i} \right)\)

\(= 2\left( {\cos {\pi  \over 3} + i\sin {\pi  \over 3}} \right)\)

Áp dụng câu a) ta có: \(\overline z  = 2\left( {\cos \left( { - {\pi  \over 3}} \right) + i\sin \left( { - {\pi  \over 3}} \right)} \right)\)

\( - z = 2\left( {\cos {{4\pi } \over 3} + i\sin {{4\pi } \over 3}} \right);\)

\({1 \over {\overline z }} = {1 \over 2}\left( {\cos {\pi  \over 3} + i\sin {\pi  \over 3}} \right)\)

\(\eqalign{  & kz = 2k\left( {\cos {\pi  \over 3} + i\sin {\pi  \over 3}} \right)\,\,\text{nếu}\,\,k > 0  \cr  & kz =  - 2k\left( {\cos {{4\pi } \over 3} + i\sin {{4\pi } \over 3}} \right)\,\text{nếu}\,\,k < 0 \cr} \)

Bài 28 trang 205 SGK giải tích 12 nâng cao

Viết các số phức sau dưới dạng lượng giác:

\(\eqalign{
& a)\,\,1 - i\sqrt 3 ;\,\,1 + i;\,\,(1 - i\sqrt 3 )(1 + i);\,\,{{1 - i\sqrt 3 } \over {1 + i}}; \cr 
& b)\,\,2i\left( {\sqrt 3 - i} \right); \cr 
& c)\,\,{1 \over {2 + 2i}}; \cr 
& d)\,\,z = \sin \varphi + i\cos \varphi \,(\varphi \in\mathbb R) \cr} \)

Giải

\(\eqalign{
& a)\,\,1 - i\sqrt 3 = 2\left( {{1 \over 2} - {{\sqrt 3 } \over 2}i} \right) \cr&= 2\left( {\cos \left( { - {\pi \over 3}} \right) + i\sin \left( { - {\pi \over 3}} \right)} \right);\,\,\,\,\, \cr 
& \,\,\,\,\,\,\,\,1 + i = \sqrt 2 \left( {{1 \over {\sqrt 2 }} + {1 \over {\sqrt 2 }}i} \right) \cr&= \sqrt 2 \left( {\cos \left( {{\pi \over 4}} \right) + i\sin \left( {{\pi \over 4}} \right)} \right);\, \cr 
& \,\,\,\,\,\,\,\,(1 - i\sqrt 3 )(1 + i) \cr&= 2\sqrt 2 \left( {{1 \over 2} - {{\sqrt 3 } \over 2}i} \right)\left( {{1 \over {\sqrt 2 }} + {1 \over {\sqrt 2 }}i} \right) \cr 
&  = 2\sqrt 2 \left( {\cos \left( { - {\pi \over 3}} \right) + i\sin \left( { - {\pi \over 3}} \right)} \right).\cr&\left( {\cos {\pi \over 4} + i\sin {\pi \over 4}} \right) \cr 
& = 2\sqrt 2 \left[ {\cos \left( {{\pi \over 4} - {\pi \over 3}} \right) + i\sin \left( {{\pi \over 4} - {\pi \over 3}} \right)} \right] \cr 
& = 2\sqrt 2 \left[ {\cos \left( { - {\pi \over {12}}} \right) + i\sin \left( { - {\pi \over {12}}} \right)} \right];\,\, \cr 
& {{1 - i\sqrt 3 } \over {1 + i}}\cr& = \sqrt 2 \left[ {\cos \left( { - {\pi \over 3} - {\pi \over 4}} \right) + i\sin \left( { - {\pi \over 3} - {\pi \over 4}} \right)} \right] \cr 
& = \sqrt 2 \left[ {\cos \left( { - {7 \over {12}}\pi } \right) + i\sin \left( { - {7 \over {12}}\pi } \right)} \right]; \cr 
& b)\,\,2i = 2\left( {\cos {\pi \over 2} + i\sin {\pi \over 2}} \right) \cr 
& \,\,\,\,\,\,\,\left( {\sqrt 3 - i} \right) = 2\left( {{{\sqrt 3 } \over 2} - {1 \over 2}i} \right)\cr& = 2\left[ {\cos \left( { - {\pi \over 6}} \right) + i\sin \left( { - {\pi \over 6}} \right)} \right]; \cr 
& \,\,\,\,\,\,\,2i\left( {\sqrt 3 - i} \right) \cr&= 4\left[ {\cos \left( {{\pi \over 2} - {\pi \over 6}} \right) + i\sin \left( {{\pi \over 2} - {\pi \over 6}} \right)} \right] \cr 
&= 4\left[ {\cos \left( {{\pi \over 3}} \right) + i\sin \left( {{\pi \over 3}} \right)} \right] \cr 
& c)\,\,2 + 2i = 2\sqrt 2 \left( {{1 \over {\sqrt 2 }} + {1 \over {\sqrt 2 }}i} \right) \cr&= 2\sqrt 2 \left( {\cos {\pi \over 4} + i\sin {\pi \over 4}} \right)\, \cr 
& \Rightarrow {1 \over {2 + 2i}} = {1 \over {2\sqrt 2 }}\left[ {\cos \left( { - {\pi \over 4}} \right) + i\sin \left( { - {\pi \over 4}} \right)} \right] \cr  
& d)\,z = \,\sin \varphi + i\cos \varphi \cr&= \,\cos \left( {{\pi \over 2} - \varphi } \right) + i\sin\left( {{\pi \over 2} - \varphi } \right)(\varphi \in \mathbb R) \cr} \)

Bài 29 trang 206 SGK Giải tích 12 Nâng cao

Dùng công thức khai triển nhị thức Niu-tơn \({\left( {1 + i} \right)^{19}}\) và công thức Moa-vrơ để tính 

\(C_{19}^0 - C_{19}^2 + C_{19}^4 - ... + C_{19}^{16} - C_{19}^{18}.\)

Giải

Theo nhị thức Niu-tơn ta có:

\({\left( {1 + i} \right)^{19}} = (C_{19}^0 + C_{19}^2{i^2} + C_{19}^4{i^2} + ... + C_{19}^{16}{i^2} \)

\(+ C_{19}^{18}{i^2}) + (C_{19}^1i + C_{19}^3{i^3} + ... + C_{19}^{19})\)

Phần thực ở vế phải là: \(C_{19}^0 - C_{19}^2 + C_{19}^4 - ... + C_{19}^{16} - C_{19}^{18}.\)

Mặt khác:

\(\eqalign{
& {\left( {1 + i} \right)^{19}} = {\left[ {\sqrt 2 \left( {\cos {\pi \over 4} + i\sin {\pi \over 4}} \right)} \right]^{19}} \cr&= {\left( {\sqrt 2 } \right)^{19}}\left( {\cos {{19\pi } \over 4} + i\sin {{19\pi } \over 4}} \right) \cr 
&  = {\left( {\sqrt 2 } \right)^{19}}\left( { - {{\sqrt 2 } \over 2} + i{{\sqrt 2 } \over 2}} \right) = - {2^9} + {2^9}i \cr 
& \Rightarrow C_{19}^0 - C_{19}^2 + C_{19}^4 - ... + C_{19}^{16} - C_{19}^{18} =- {2^9} \cr&= - 512. \cr} \)

Bài 30 trang 206 SGK giải tích 12 nâng cao

Gọi M, M’ là các điểm trong mặt phẳng phức theo thứ tự biểu diễn các số \(z = 3 + i;\,z' = \left( {3 - \sqrt 3 } \right) + \left( {1 + 3\sqrt 3 } \right)i.\)

a) Tính \({{z'} \over z};\)

b) Chứng minh rằng hiệu số acgumen của z’ với acgumen của z là một số đo của góc lượng giác \(\left( {OM,OM'} \right)\). Tính số đo đó.

Giải

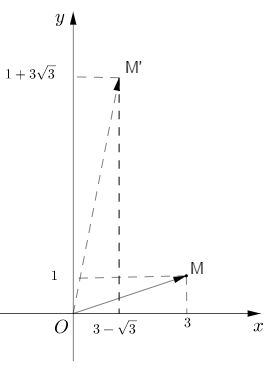
\(a)\,{{z'} \over z} = {{\left[ {3 - \sqrt 3  + \left( {1 + 3\sqrt 3 } \right)i} \right]\left( {3 - i} \right)} \over {10}} = 1 + \sqrt 3 i\)

b) Xét tia Ox thì ta có: \(sđ\left( {OM,OM'} \right) = sđ\left( {Ox,OM'} \right) - sđ\left( {Ox,OM} \right)\)

                             \( = \varphi ' - \varphi  = acgumen{{z'} \over z}\) (sai khác \(k2\pi \))

(trong đó \(\varphi \) và \(\varphi '\) theo thứ tự là acgumen của z và z’).

Từ đó do \({{z'} \over z} = 1 + \sqrt 3 i\) có acgumen là \({\pi  \over 3} + k2\pi \,\,\left( {k \in Z} \right)\), nên góc lượng giác \(\left( {OM,OM'} \right)\) có số đo \({\pi  \over 3} + k2\pi \,\,\left( {k \in\mathbb Z} \right)\)

Giaibaitap.me