Bài 5 trang 70 SGK Hình học 10 nâng cao

Cho hình vuông ABCD cạnh a. Gọi N là trung điểm của CD, M là điểm trên AC sao cho \(AM = {1 \over 4}AC.\)

a)Tính các cạnh của tam giác BMN.

b) Có nhận xét gì về tam giác BMN ? Tính diện tích tam giác đó.

c) Gọi I là giao điểm của  BN và AC. Tính CI.

d) Tính bán kính đường tròn ngoại tiếp tam giác BDN.

Hướng dẫn trả lời

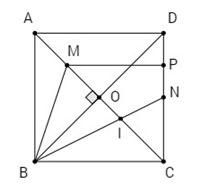
a) Gọi O là tâm của hình bình hành ABCD thì M là trung điểm AO.

\(\eqalign{
& B{N^2} = B{C^2} + N{C^2} \cr
& \,\,\,\,\,\,\,\,\,\,\, = {a^2} + {{{a^2}} \over 4} = {{5{a^2}} \over 4}\,\, \Rightarrow \,\,BN = {{a\sqrt 5 } \over 2} \cr
& B{M^2} = B{O^2} + O{M^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = {\left( {{{a\sqrt 2 } \over 2}} \right)^2} + {\left( {{{a\sqrt 2 } \over 4}} \right)^2} = {{5{a^2}} \over 8} \cr
& \,\,\,\, \Rightarrow \,\,BM = {{a\sqrt {10} } \over 4} \cr} \)

Kẻ MP // AD ta có

 \(M{N^2} = M{P^2} + P{N^2} = {\left( {{{3a} \over 4}} \right)^2} + {\left( {{a \over 4}} \right)^2} = {{10{a^2}} \over {16}}\,\,\)

\(\Rightarrow \,\,MN = {{a\sqrt {10} } \over 4}\)

b) Ta có

\(MB = MN\,,\,\,B{N^2} = M{B^2} + M{N^2}\) nên tam giác BMN vuông cân tại M. Diện tích tam giác BMN là

                       \({S_{BMN}} = {1 \over 2}M{N^2} = {1 \over 2}.{{10{a^2}} \over {16}} = {{5{a^2}} \over {16}}\)

c) Ta có I là trọng tâm tam giác BCD nên \(IC = {2 \over 3}IO = {2 \over 3}.a.{{\sqrt 2 } \over 2} = {{a\sqrt 2 } \over 3}\).

d) Gọi R là bán kính đường tròn ngoại tiếp tam giác BDN.

Áp dụng định lí sin ta có

            \({{BN} \over {\sin \widehat {BDN}}} = 2R\,\, \Rightarrow \,\,R = \,{{BN} \over {2\sin {{45}^0}}} = {{a\sqrt 5 } \over 2}.{1 \over {\sqrt 2 }} = {{a\sqrt {10} } \over 4}\)

Bài 6 trang 70 SGK Hình học 10 nâng cao

Trong mặt phẳng tọa độ, cho \(\overrightarrow e  = (4\,;\,1)\) và \(\overrightarrow f  = (1\,;\,4)\).

a) Tìm góc giữa các vec tơ \(\overrightarrow e \) và \(\overrightarrow f \).

b) Tìm m để vec tơ \(\overrightarrow a  = \overrightarrow e  + m\overrightarrow f \) vuông góc với trục hoành.

c) Tìm n để vec tơ \(\overrightarrow b  = n\overrightarrow e  + \overrightarrow f \) tạo với vec tơ \(\overrightarrow i  + \overrightarrow j \) một góc \({45^0}\).

Hướng dẫn trả lời

a) Góc giữa các vectơ \(\overrightarrow e \) và \(\overrightarrow f \)

\(\eqalign{
& \cos (\overrightarrow {e\,} \,,\,\overrightarrow f ) = {{\overrightarrow {e\,} .\,\overrightarrow f } \over {|\overrightarrow {e\,} |.\,|\overrightarrow {f|} }} = {{4.1 + 1.4} \over {\sqrt {{4^2} + {1^2}} .\sqrt {{1^2} + {4^2}} }} = {8 \over {17}} \cr
& \Rightarrow \,\,\,(\overrightarrow {e\,} \,,\,\overrightarrow f ) \approx {61^0}{56'} \cr} \)

b) Ta có \(\overrightarrow a  = \overrightarrow {e\,}  + m\overrightarrow {f\,}  = (4 + m\,;\,1 + 4m)\).

\(\overrightarrow a  = \overrightarrow e  + m\overrightarrow f \) vuông góc với trục hoành \( \Leftrightarrow \,\,\overrightarrow a .\,\overrightarrow i  = 0\,\, \Leftrightarrow \,\,4 + m = 0\,\, \Leftrightarrow m =  - 4\) .

c) Ta có

\(\eqalign{
& \,\,\overrightarrow b = n\overrightarrow e + \overrightarrow f = (4n + 1\,;\,n + 4)\,;\,\,\overrightarrow i + \overrightarrow j = (1\,;\,1) \cr
& \,\,(\overrightarrow b \,;\,\overrightarrow i + \overrightarrow j ) = {45^0}\,\,\,\,\,\,\,\, \Rightarrow \,\,\cos {45^0} = {{\overrightarrow b \,.\,(\,\overrightarrow i + \overrightarrow j )} \over {|\overrightarrow b \,|.\,|\,\overrightarrow i + \overrightarrow j |}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\,{{\sqrt 2 } \over 2} = {{(4n + 1) + (n + 4)} \over {\sqrt {{{(4n + 1)}^2} + {{(n + 4)}^2}} .\,\sqrt {{1^2} + {1^2}} }} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\,{(4n + 1)^2} + {(n + 4)^2} = {(5n + 5)^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\,8{n^2} + 34n + 8 = 0\,\, \Rightarrow \,\,n = {{ - 1} \over 4}\,;\,\,n = - 4. \cr} \)

Thử lại với \(n =  - 4\) ta có \(\overrightarrow b  = ( - 15\,;\,0)\).

                              \(\cos (\overrightarrow b \,;\,\overrightarrow i  + \overrightarrow j ) = {{ - 15} \over {15.\sqrt 2 }} =  - {1 \over {\sqrt 2 }}\) (loại)

Với \(n = {{ - 1} \over 4}\,\,;\,\,\overrightarrow b  = \left( {0\,;\,{{15} \over 4}} \right)\)

                               \(\cos (\overrightarrow b \,;\,\overrightarrow i  + \overrightarrow j ) = {1 \over {\sqrt 2 }}\) (nhận).

Vậy \(n = {{ - 1} \over 4}\).

Bài 7 trang 70 SGK Hình học 10 nâng cao

Cho tam giác ABC. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là

\({b^2} + {c^2} = 5{a^2}\) 

Hướng dẫn trả lời

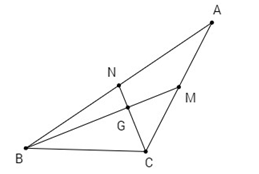
Gọi G  là giao điểm của hai trung tuyến BM, CN.

Áp dụng công thức tính trung tuyến ta có      

\(\eqalign{
& G{B^2} = {4 \over 9}B{M^2} = {1 \over 9}(2{a^2} + 2{c^2} - {b^2}) \cr
& G{C^2} = {4 \over 9}C{N^2} = {1 \over 9}(2{a^2} + 2{b^2} - {c^2}) \cr} \)

Do đó \(BM \bot CN\,\, \Leftrightarrow \,\,B{G^2} + C{G^2} = B{C^2}\)

\(\eqalign{
& \Leftrightarrow \,\,{1 \over 9}(2{a^2} + 2{c^2} - {b^2}) + {1 \over 9}(2{a^2} + 2{b^2} - {c^2}) = {a^2} \cr
& \Leftrightarrow \,\,4{a^2} + {b^2} + {c^2} = 9{a^2} \cr
& \Leftrightarrow \,\,{b^2} + {c^2} = 5{a^2} \cr} \)

Bài 8 trang 70 SGK Hình học 10 nâng cao

Trong các tam giác có hai cạnh là a và b, tìm tam giác có diện tích lớn nhất.

Hướng dẫn trả lời

Ta có diện tích tam giác ABC là \({S_{ABC}} = {1 \over 2}a.b.\sin C\).

Mà \(\sin C \le 1\)  nên \({S_{ABC}} \le {1 \over 2}a.b\).

Do đó S lớn nhất khi \(\sin C = 1\), tức là tam giác ABC vuông tại C.

Giaibaitap.me