Bài 3.50 trang 162 Sách bài tập (SBT) Toán Hình Học 10

Cho đường tròn  (C): \({x^2} + {y^2} - 2x - 6y + 6 = 0\) và điểm M(2;4).

a) Chứng minh rằng điểm M nằm trong  (C) ;

b) Viết phương trình đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm A, B sao cho M là trung điểm của đoạn AB.

Gợi ý làm bài

a) (C): \({x^2} + {y^2} - 2x - 6y + 6 = 0 \Rightarrow \) 

(C) có

\(\left\{ \matrix{
I(1;3) \hfill \cr
\,R = 2 \hfill \cr} \right.\,\)

(R là bán kính)

\(IM = \sqrt 2  < R \Rightarrow \) M nằm trong (C)

 b) Đường thẳng d cắt đường tròn (C) tại hai điểm A, B sao cho M là trung điểm của đoạn thẳng \(AB \Rightarrow d \bot IM\) tại M

Phương trình đường thẳng:

d: - qua M(2;4)

    - nhận \(\overrightarrow {{\rm{IM}}} {\rm{ = (1;1)}}\) làm vectơ pháp tuyến

\( \Rightarrow d:1.(x - 2) + 1.(y - 4) = 0\)

\( \Rightarrow d:x + y - 6 = 0.\)

Bài 3.51 trang 162 Sách bài tập (SBT) Toán Hình Học 10

Trong mặt phẳng tọa độ Oxy cho elip (E) : \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\)

a) Xác định độ dài các trục, tiêu cự của elip (E) ;

b) Tìm các điểm M thuộc (E) sao cho \({1 \over {M{F_1}}} + {1 \over {M{F_2}}} = {8 \over {{F_1}{F_2}}}\).

Gợi ý làm bài

\((E):{{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\)

a) Ta có :  

\(\left\{ \matrix{
{a^2} = 25 \Rightarrow a = 5 \hfill \cr
{b^2} = 9 \Rightarrow b = 3 \hfill \cr} \right.\)

\( \Rightarrow {c^2} = {a^2} - {b^2} = 25 - 9 = 16 \Rightarrow c = 4.\)

Độ dài trục lớn : \({A_1}{A_2} = 2a = 10\); Độ dài trục bé : \({B_1}{B_2} = 2b = 6\). Tiêu cự : \({F_1}{F_2} = 2c = 8\)

b) M thuộc \((E) \Rightarrow \left\{ \matrix{
M{F_1} = a + {c \over a}x = 5 + {4 \over 5}x \hfill \cr
M{F_2} = a - {c \over a}x = 5 - {4 \over 5}x \hfill \cr} \right.\)

\({1 \over {M{F_1}}} + {1 \over {M{F_2}}} = {8 \over {{F_1}{F_2}}} \Leftrightarrow 25 - {{16} \over {25}}{x^2} = 10\)

\( \Leftrightarrow x \pm {{5\sqrt {15} } \over 4} \Rightarrow y =  \pm {3 \over 4}\)

Vậy : có bốn điểm thỏa mãn yêu cầu bào toán là: \(M\left( { \pm {{5\sqrt {15} } \over 4}; \pm {3 \over 4}} \right).\)

Bài 3.52 trang 163 Sách bài tập (SBT) Toán Hình Học 10

Trong mặt phẳng tọa độ Oxy cho đường tròn (C) : \({x^2} + {y^2} + 4x + 4y + 6 = 0\) và đường thẳng \(\Delta :x + my - 2m + 3 = 0\) với m là tham số thực.

a) Tìm tọa độ tâm I và bán kính R của đường tròn (C) ;

b) Tìm m để  cắt (C)  tại hai điểm phân biệt sao cho diện tích tam giác IAB đạt giá trị lớn nhất. 

Gợi ý làm bài

(Xem hình 3.12)

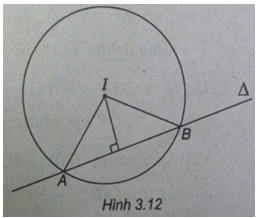
a) Đường tròn (C)  có tâm I(-2;-2) và bán kính \(R = \sqrt {2.} \)

b) Diện tích tam giác IAB là : 

\(S = {1 \over 2}IA.IB\sin AIB \le {1 \over 2}{R^2} = 1.\)

S lớn nhất \( \Leftrightarrow S = 1\)

\( \Leftrightarrow \sin AIB = 1\)

\( \Leftrightarrow IA \bot IB\)

\( \Leftrightarrow d\left( {I,\Delta } \right) = {R \over {\sqrt 2 }}\)

\( \Leftrightarrow {{\left| { - 2 - 2m - 2m + 3} \right|} \over {\sqrt {1 + {m^2}} }} = 1\)

\( \Leftrightarrow {\left( {1 - 4m} \right)^2} = 1 + {m^2}\)

\( \Leftrightarrow 15{m^2} - 8m = 0\)

\( \Leftrightarrow m = 0$ hay $m = {8 \over {15}}\)

Bài 3.53 trang 163 Sách bài tập (SBT) Toán Hình Học 10

Trong mặt phẳng Oxy cho tam giác ABC cân tại A có A(-1;4) và các đỉnh B, C thuộc đường thẳng : \(\Delta :x - y - 4 = 0\)

a) Tính khoảng cách từ A đến đường thẳng \(\Delta \)

b) Xác định tọa độ các điểm B và C, biết diện tích tam giác ABC bằng 18.

Gợi ý làm bài

a) Gọi H là hình chiếu của A trên , suy ra H là trung điểm của BC.

\(AH = d(A,BC) = {9 \over {\sqrt 2 }}$

b) \(BC = {{2{S_{\Delta ABC}}} \over {AH}} = 4\sqrt 2 .\)

\(AB = AC = \sqrt {A{H^2} + {{B{C^2}} \over 4}}  = \sqrt {{{97} \over 2}} .\)

Tọa độ điểm B và C là nghiệm của hệ : 

\(\left\{ \matrix{
{\left( {x + 1} \right)^2} + {(y - 4)^2} = {{97} \over 2} \hfill \cr
x - y - 4 = 0\,. \hfill \cr} \right.\)

Giải hệ ta được $\left( {x;y} \right) = \left( {{{11} \over 2};{3 \over 2}} \right)$ hoặc $\left( {x;y} \right) = \left( {{3 \over 2}; - {5 \over 2}} \right)\)

Vậy \(B\left( {{{11} \over 2};{3 \over 2}} \right)\,,\,C\left( {{3 \over 2}; - {5 \over 2}} \right)$ hoặc $B\left( {{3 \over 2}; - {5 \over 2}} \right)\,,C\left( {{{11} \over 2};{3 \over 2}} \right)\,.\)

Giaibaitap.me