Bài 1 trang 196 Sách bài tập (SBT) Toán Hình học 10

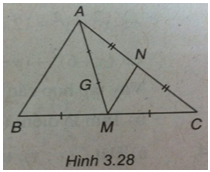
Trong mặt phẳng  Oxy cho tam giác ABC, biết đỉnh A(1 ; 1) và tọa độ trọng tâm G(1 ; 2). Cạnh AC và đường trung trực của nó lần lượt có phương trình là x + y - 2 = 0 và  - x + y - 2 = 0. Các điểm M và N lần lượt là trung điểm của BC và AC.

a) Hãy tìm tọa độ các điểm M và N.

b) Viết phương trình hai đường thẳng chứa hai cạnh AB và BC. 

Gợi ý làm bài

(h.3.28) 

a) \(\eqalign{
& \overrightarrow {AM} = {3 \over 2}\overrightarrow {AG} \cr
& \Leftrightarrow \left\{ \matrix{
{x_M} - 1 = {3 \over 2}(1 - 1) \hfill \cr
{y_M} - 1 = {3 \over 2}(2 - 1) \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
{x_M} = 1 \hfill \cr
{y_M} = {5 \over 2}. \hfill \cr} \right. \cr} \)

Vậy M có tọa độ là \(\left( {1;{5 \over 2}} \right)\)

Điểm N(x ; y) thỏa mãn hệ phương trình

\(\left\{ \matrix{
x + y = 2 \hfill \cr
- x + y = 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 0 \hfill \cr
y = 2. \hfill \cr} \right.\)

b) \(\eqalign{
& \overrightarrow {AB} = 2\overrightarrow {NM} \cr
& \Leftrightarrow \left\{ \matrix{
{x_B} - 1 = 2(1 - 0) \hfill \cr
{y_B} - 1 = 2\left( {{5 \over 2} - 2} \right) \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
{x_B} = 3 \hfill \cr
{y_B} = 2. \hfill \cr} \right. \cr} \)

Đường thẳng chứa cạnh AB đi qua hai điểm A(1 ;1) và B(3 ; 2) nên có phương trình : x - 2y + 1=0.

Đường thẳng chứa cạnh BC đi qua hai điểm B(3 ; 2) và $M\left( {1;{5 \over 2}} \right)$ nên có phương trình:

x + 4y - 11 = 0

Bài 2 trang 196 Sách bài tập (SBT) Toán Hình học 10

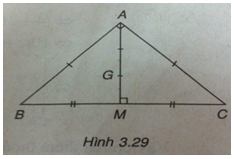
Trong mặt phẳng  Oxy cho tam giác ABC có \(AB = AC,\,\widehat {BAC} = {90^ \circ }\). Biết M(1 ; -1) là trung điểm cạnh BC và \(G\left( {{2 \over 3};0} \right)\) là trọng tâm tam giác ABC.

Tìm tọa độ các đỉnh A, B, C.

Gợi ý làm bài

(h.3.29)

\(\eqalign{
& \overrightarrow {MA} = 3\overrightarrow {MG} \Leftrightarrow \left\{ \matrix{
{x_A} - 1 = 3\left( {{2 \over 3} - 1} \right) \hfill \cr
{y_A} + 1 = 3(0 + 1) \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
{x_A} = 0 \hfill \cr
{y_A} = 2. \hfill \cr} \right. \cr} \)

Vậy A có tọa độ (0 ; 2).

Đặt B(x ; y) ta có : 

\(\eqalign{
& \,\,\,\,\,\,\,\left\{ \matrix{
\overrightarrow {MB} \bot \overrightarrow {MA} \hfill \cr
M{B^2} = M{A^2} \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
\left( {x - 1} \right)\left( {0 - 1} \right) + \left( {y + 1} \right)\left( {2 + 1} \right) = 0 \hfill \cr
{\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = 1 + 9 \hfill \cr} \right. \cr} \)

\(\Leftrightarrow \left\{ \matrix{
x = 3y + 4 \hfill \cr
{(3y + 3)^2} + {(y + 1)^2} = 10 \hfill \cr} \right.\)

\(\eqalign{
& \Leftrightarrow \left\{ \matrix{
x = 3y + 4 \hfill \cr
{(3y + 3)^2} + {(y + 1)^2} = 10 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
x = 3y + 4 \hfill \cr
10{y^2} + 20y = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
y = 0,x = 4 \hfill \cr
y = - 2,x = - 2 \hfill \cr} \right. \cr} \)

Vậy ta có tọa độ của điểm B và C như sau : B(4 ; 0), C(-2 ; -2) hoặc B(-2 ; -2), C(4 ; 0).

Bài 3 trang 196 Sách bài tập (SBT) Toán Hình học 10

Cho ba điểm A(1 ; 2), B(-3 ; 1), C(4 ; -2).

a) Chứng minh rằng tập hợp các điểm M(x;y) thỏa mãn \(M{A^2} + M{B^2} = M{C^2}\) là một đường tròn.

b) Tìm tọa độ tâm và bán kính của đường tròn nói trên.

Gợi ý làm bài

a) \(M{A^2} + M{B^2} = M{C^2}\)

\( \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {x + 3} \right)^2} + {\left( {y - 1} \right)^2} = {\left( {x - 4} \right)^2} + {\left( {y + 2} \right)^2}\)

\(\Leftrightarrow {x^2} + {y^2} + 12x - 10y - 5 = 0\)

\( \Leftrightarrow {\left( {x + 6} \right)^2} + {\left( {y - 5} \right)^2} = 66.\)

Vậy tập hợp các điểm M là một đường tròn.

b) Tâm là điểm (-6 ; 5) bán kính bằng \(\sqrt {66} \)

Bài 4 trang 197 Sách bài tập (SBT) Toán Hình học 10

Cho hai điểm A(3 ; -1), B(-1 ; -2) và đường thẳng d có phương trình x + 2y + 1 = 0

a) Tìm tọa độ điểm C trên đường thẳng d sao cho tam giác ABC là tam giác cân tại C.

b) Tìm tọa độ điểm M trên đường thẳng d sao cho tam giác AMB vuông tại M.

Gợi ý làm bài

a) Đặt C(x ; y), ta có : \(C \in d \Leftrightarrow x =  - 2y - 1\). Vậy C( - 2y - 1;y).

Tam giác ABC cân tại C khi và chỉ khi

CA = CB \( \Leftrightarrow C{A^2} = C{B^2}\)

\( \Leftrightarrow {\left( {3 + 2y + 1} \right)^2} + {\left( { - 1 - y} \right)^2} = {\left( { - 1 + 2y + 1} \right)^2} + {\left( { - 2 - y} \right)^2}\)

\( \Leftrightarrow {\left( {4 + 2y} \right)^2} + {\left( {1 + y} \right)^2} = 4{y^2} + {\left( {2 + y} \right)^2}\)

Giải ra ta được \(y =  - {{13} \over {14}}.\)

\(x =  - 2\left( {{{ - 13} \over {14}}} \right) - 1 = {{13} \over 7} - 1 = {6 \over 7}.\)

Vậy C có tọa độ là \(\left( {{6 \over 7}; - {{13} \over {14}}} \right)\)

b) Xét điểm M( - 2t - 1;t) trên d, ta có :

\(\widehat {AMB} = {90^ \circ } \Leftrightarrow A{M^2} + B{M^2} = A{B^2}\)

\( \Leftrightarrow {\left( {4 + 2t} \right)^2} + {\left( {1 + t} \right)^2} + 4{t^2} + {\left( {2 + t} \right)^2} = 17\)

\( \Leftrightarrow 10{t^2} + 22t + 4 = 0 \Leftrightarrow 5{t^2} + 11t + 2 = 0\)

\( \Leftrightarrow \left[ \matrix{
t = - {1 \over 5} \hfill \cr
t = - 2. \hfill \cr} \right.\)

Vậy có hai điểm thỏa mãn đề bài là \({M_1}\left( { - {3 \over 5}; - {1 \over 5}} \right)\) và \({M_2}\left( {3; - 2} \right)\)

Giaibaitap.me