Bài 9 trang 197 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \({(x - 5)^2} + {(y - 3)^2} = 4\). Và điểm A(1 ; 2), một đường thẳng d đi qua A và cắt đường tròn (C) theo một dây cung MN có độ dài bằng \(2\sqrt 3 \). Viết phương trình của d.

Gợi ý làm bài

(Xem hình 3.32)

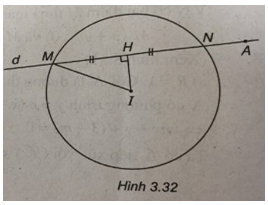
Đường tròn (C) có tâm I(5 ; 3) và có bán kính R = 2.

Gọi H là trung điểm của MN. Ta có

\(IH \bot MN\) và \(MH = {{MN} \over 2} = \sqrt 3 \)

\(IH = \sqrt {I{M^2} - M{H^2}}  = \sqrt {4 - 3}  = 1.\)

Phương trình đường thẳng d có dạng : 

\(y - 2 = k(x - 1) \Leftrightarrow kx - y + 2 - k = 0.\)

Ta có IH = 1

\( \Leftrightarrow {{\left| {5k - 3 + 2 - k} \right|} \over {\sqrt {{k^2} + 1} }} = 1\)

\(\eqalign{
& \Leftrightarrow \left| {4k - 1} \right| = \sqrt {{k^2} + 1} \cr
& \Leftrightarrow {\left( {4k - 1} \right)^2} = {k^2} + 1 \cr} \)

\(\eqalign{
& \Leftrightarrow 15{k^2} - 8k = 0 \cr
& \Leftrightarrow \left[ \matrix{
k = 0 \hfill \cr
k = {8 \over {15}} \hfill \cr} \right. \cr} \)

Vậy có hai điểm d thỏa mãn đề bài.

Đó là \({d_1}:y - 2 = 0\)

\(\eqalign{
& {d_2}:y - 2 = {8 \over {15}}\left( {x - 1} \right) \cr
& \Leftrightarrow 8x - 15y + 22 = 0. \cr} \)

Bài 10 trang 198 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng tọa độ Oxy, cho elip (E): \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\). Gọi hai tiêu điểm của (E) lần lượt là \({F_1},{F_2}\) và M thuộc (E) sao cho \(\widehat {{F_1}M{F_2}} = {60^ \circ }\) . Tìm tọa độ điểm M và tính diện tích tam giác  \(M{F_1}{F_2}\)

Gợi ý làm bài

(Xem hình 3.33)

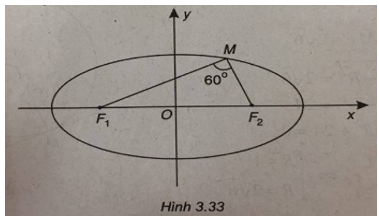
Elip (E) có phương trình chính tắc: \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1.\)

Ta có : a = 5, b = 3. Suy ra \({c^2} = {a^2} - {b^2} = 25 - 9 = 16.\)

Vậy c = 4.

Xét điểm M(x;y) thuộc elip, ta có:

\(\left\{ \matrix{
{F_1}M = a + {c \over a}x = 5 + {4 \over 5}x \hfill \cr
{F_2}M = a - {c \over a}x = 5 - {4 \over 5}x \hfill \cr} \right.\)

Áp dụng định lí côsin trong tam giác \({F_1}M{F_2}\) ta có:

\({F_1}F_2^2 = MF_1^2 + MF_2^2 - 2M{F_1}.M{F_2}\cos {60^ \circ }\)

\( \Leftrightarrow 4{c^2} = {\left( {5 + {4 \over 5}x} \right)^2} + {\left( {5 - {4 \over 5}x} \right)^2} - 2\left( {25 - {{16} \over {25}}{x^2}} \right).{1 \over 2}\)

\(\Leftrightarrow 64 = 25 + {{48} \over {25}}{x^2} \Leftrightarrow {x^2} = {{25} \over {16}}.13 \Leftrightarrow x =  \pm {5 \over 4}\sqrt {13} \,\,(1)\)

Ta lại có: \(M \in \left( E \right) \Rightarrow {{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\,\,\,\,\,(2)\)

Thay (1) vào phương trình (2) ta được:

\({{{y^2}} \over 9} = 1 - {{13} \over {16}} \Leftrightarrow {y^2} = {9 \over {16}}.3 \Leftrightarrow y =  \pm {3 \over 4}\sqrt 3 .\)

Vậy có bốn điểm M thỏa mãn đề bài. Chúng có tọa độ là \(\left( { \pm {5 \over 4}\sqrt {13} ; \pm {3 \over 4}\sqrt 3 } \right).\)

Bài 11 trang 198 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng tọa độ Oxy, cho ba điểm I(2 ; 4), B(1 ; 1), C(5 ; 5). Tìm điểm A sao cho I là tâm đường tròn nội tiếp tam giác ABC.

Gợi ý làm bài

(Xem hình 3.34)

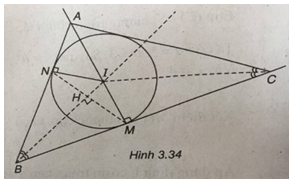
Ta có : \(IB = \sqrt {{{\left( {1 - 2} \right)}^2} + {{\left( {1 - 4} \right)}^2}}  = \sqrt {10} \)

\(\eqalign{
& IC = \sqrt {{{(5 - 2)}^2} + {{(5 - 4)}^2}} = \sqrt {10} \cr
& IB = IC \Rightarrow AB = AC. \cr} \)

Gọi M là trung điểm của BC, ta có M(3 ; 3).

Phương trình đường thẳng \(IM:x + y - 6 = 0\,\,\,\,\,\,\,\,\,\,(1)\)

Phương trình đường thẳng \(IB:3x - y - 2 = 0\,\,\,\,\,\,\,\,\,(2)\)

Gọi N là điểm đối xứng với M qua đường thẳng IB. Đặt N(x;y), ta có tọa độ trung điểm H của MN là \(\left( {{{x + 3} \over 2};{{y + 3} \over 2}} \right).\)

\(\overrightarrow {MN}  = (x - 3;y - 3)\)

\(\overrightarrow {BI}  = (1;3)\)

Ta có: \(\left\{ \matrix{
\overrightarrow {MN} .\overrightarrow {BI} = 0 \hfill \cr
H \in IB \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{
x - 3 + 3(y - 3) = 0 \hfill \cr
3\left( {{{x + 3} \over 2}} \right) - \left( {{{y + 3} \over 2}} \right) - 2 = 0 \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{
x + 3y - 12 = 0 \hfill \cr
3x - y + 2 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = {3 \over 5} \hfill \cr
y = {{19} \over 5}. \hfill \cr} \right.\)

Vậy \(N\left( {{3 \over 5};{{19} \over 5}} \right).\)

Ta có B(1 ; 1). Phương trình đường thẳng BN: 7x + y - 8 = 0.

Điểm A là giao của hai đường thẳng BN và IM nên tọa độ của A là nghiệm của hệ phương trình

\( \Leftrightarrow \left\{ \matrix{
7x + y - 8 = 0 \hfill \cr
x + y - 6 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = {1 \over 3} \hfill \cr
y = {{17} \over 3} \hfill \cr} \right.\)

Vậy tọa độ điểm A là \(\left( {{1 \over 3};{{17} \over 3}} \right).\)

Bài 12 trang 198 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng tọa độ Oxy, cho elip (E): \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\left( {a > b > 1} \right).\) Một góc vuông uOv (vuông tại O) quay quanh gốc O, cắt elip (E) tại M và N. Chứng minh rằng \({1 \over {O{M^2}}} + {1 \over {O{N^2}}}\) không đổi, từ đó suy ra MN luôn tiếp xúc với một đường tròn cố định.

Gợi ý làm bài

(Xem hình 3.35)

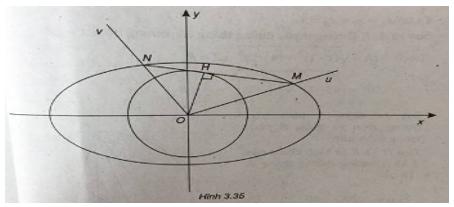
Gọi y = kx và \(y =  - {1 \over k}x\) là phương trình của Ou và Ov. 

Phương trình hoành độ giao điểm của Ou và elip (E):

\({{{x^2}} \over {{a^2}}} + {{{k^2}{x^2}} \over {{b^2}}} = 1 \Leftrightarrow x_M^2 = {{{a^2}{b^2}} \over {{b^2} + {k^2}{a^2}}}.\)

Ta có : 

\(\eqalign{
& O{M^2} = x_M^2 + y_M^2 \cr
& = x_M^2 + {k^2}x_M^2 = x_M^2({k^2} + 1) \cr
& = {{{a^2}{b^2}(1 + {k^2})} \over {{b^2} + {k^2}{a^2}}} \cr} \)

.............

Suy ra : \({1 \over {O{M^2}}} = {{{b^2} + {k^2}{a^2}} \over {{a^2}{b^2}(1 + {k^2})}}.\)

Tương tự:

\(\eqalign{
& {1 \over {O{N^2}}} = {{{b^2} + {1 \over {{k^2}}}{a^2}} \over {{a^2}{b^2}\left( {1 + {1 \over {{k^2}}}} \right)}} \cr
& = {{{a^2} + {k^2}{b^2}} \over {{a^2}{b^2}(1 + {k^2})}}. \cr} \)

Suy ra: 

\(\eqalign{
& {1 \over {O{M^2}}} + {1 \over {O{N^2}}} \cr
& = {{{a^2} + {b^2} + {k^2}\left( {{a^2} + {b^2}} \right)} \over {{a^2}{b^2}\left( {1 + {k^2}} \right)}} \cr
& = {{{a^2} + {b^2}} \over {{a^2}{b^2}}}. \cr} \)

Vậy \({1 \over {O{M^2}}} + {1 \over {O{N^2}}}\) không đổi.

Vẽ đường cao OH của tam giác vuông OMN.

Ta có : \({1 \over {O{H^2}}} = {1 \over {O{M^2}}} + {1 \over {O{N^2}}} = {{{a^2} + {b^2}} \over {{a^2}{b^2}}}.\)

Suy ra: \(OH = {{ab} \over {\sqrt {{a^2} + {b^2}} }} = R\) không đổi

Vậy MN luôn tiếp xúc với đường tròn cố định tâ O bán kính \(R = {{ab} \over {\sqrt {{a^2} + {b^2}} }}.\)

Giaibaitap.me