Bài 3.66 trang 164 Sách bài tập (SBT) Toán Hình Học 10

Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có tâm $I\left( {{1 \over 2};0} \right)$ phương trình đường thẳng AB là : x - 2y + 2 = 0 và AB = 2AD. Tìm tọa độ các đỉnh A, B, C, D biết rằng đỉnh A có hoành độ âm.

Gợi ý làm bài

(Xem hình 3.24)

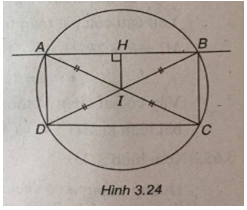
Khoảng cách từ I đến đường thẳng AB bằng 

${{\sqrt 5 } \over 2}$ $\Rightarrow AD = \sqrt 5$ và $IA = IB = {5 \over 2}.$

Do đó A, B là các giao điểm của đường thẳng AB với đường tròn tâm I và bán kính $R = {5 \over 2}.$

Vậy tọa độ A, B là nghiệm của hệ : 

$\left\{ \matrix{ x - 2y + 2 = 0 \hfill \cr {\left( {x - {1 \over 2}} \right)^2} + {y^2} = {\left( {{5 \over 2}} \right)^2} \hfill \cr} \right.$

Giải hệ ta được $A( - 2;0),B(2;2)$ (vì ${x_A} < 0$)

$\Rightarrow C\left( {3;0} \right),D\left( { - 1; - 2} \right).$

Bài 3.67 trang 164 Sách bài tập (SBT) Toán Hình Học 10

Trong mặt phẳng tọa độ Oxy,xét tam giác ABC vuông tại A, phương trình đường thẳng BC là :  $\sqrt 3 x - y - \sqrt 3  = 0$, các đỉnh A và B thuộc trục hoành và bán kính đường tròn nội tiếp tam giác bằng 2. Tìm tọa độ trọng tâm G của tam giác ABC.

Gợi ý làm bài

( Xem hình 3.25)

Ta có: $BC \cap Ox = B(1;0)$

Đặt ${x_A} = a$ ta có A(a;0) và ${x_C} = a \Rightarrow {y_C} = \sqrt 3 a - \sqrt 3 .$

Vậy $C\left( {a;\sqrt 3 a - \sqrt 3 } \right).$

Từ công thức

$\left\{ \matrix{ {x_G} = {1 \over 3}\left( {{x_A} + {x_B} + {x_C}} \right) \hfill \cr {y_G} = {1 \over 3}\left( {{y_A} + {y_B} + {y_C}} \right) \hfill \cr} \right.$

Ta có:

$G\left( {{{2a + 1} \over 3};{{\sqrt 3 \left( {a - 1} \right)} \over 3}} \right).$

Mà $AB = \left| {a - 1} \right|,AC = \sqrt 3 \left| {a - 1} \right|,BC = 2\left| {a - 1} \right|$. Do đó : 

${S_{\Delta ABC}} = {1 \over 2}AB.AC = {{\sqrt 3 } \over 2}{\left( {a - 1} \right)^2}.$

Ta có:

$\eqalign{ & r = {{2S} \over {AB + AC + BC}} \cr & = {{\sqrt 3 {{\left( {a - 1} \right)}^2}} \over {3\left| {a - 1} \right| + \sqrt 3 \left| {a - 1} \right|}} = {{\left| {a - 1} \right|} \over {\sqrt 3 + 1}} = 2. \cr}$

Vậy $\left| {a - 1} \right| = 2\sqrt 3  + 2.$

Trường hợp 1. 

${a_1} = 2\sqrt 3  + 3 \Rightarrow {G_1}\left( {{{7 + 4\sqrt 3 } \over 3};{{6 + 2\sqrt 3 } \over 3}} \right).$

Trường hợp 2. 

${a_2} =  - 2\sqrt 3  - 1 \Rightarrow {G_2}\left( {{{4\sqrt 3  - 1} \over 3};{{ - 6 - 2\sqrt 3 } \over 3}} \right).$

Bài 3.68 trang 164 Sách bài tập (SBT) Toán Hình Học 10

Trong mặt phẳng tọa độ Oxy, cho điểm C(2;0) và elip (E): ${{{x^2}} \over 4} + {{{y^2}} \over 1} = 1$. Tìm tọa độ các điểm A, B thuộc (E), biết rằng hai điểm A, B đối xứng với nhau qua trục hoành và tam giác ABC là tam giác đều.

Gợi ý làm bài

Giả sử $A\left( {{x_0};{y_0}} \right)$. Do A, B đối xứng nhau qua Ox nên $B({x_0}; - {y_0})$

Ta có : $A{B^2} = 4y_0^2$ và $A{C^2} = {\left( {{x_0} - 2} \right)^2} + y_0^2.$

Vì $A \in (E)$ nên ${{x_0^2} \over 4} + y_0^2 = 1 \Rightarrow y_0^2 = 1 - {{x_0^2} \over 4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$

Vì AB = AC nên ${\left( {{x_0} - 2} \right)^2} + y_0^2 = 4y_0^2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)$

Thay (1) vào (2) và rút gọn ta được 

$7x_0^2 - 16{x_0} + 4 = 0 \Leftrightarrow \left[ \matrix{ {x_0} = 2 \hfill \cr {x_0} = {2 \over 7}. \hfill \cr} \right.$

Với ${x_0} = 2$ thay vào (1) ta có ${y_0} = 0.$ Trường hợp này loại vì $A \equiv C.$

Với ${x_0} = {2 \over 7}$ thay vào (1) ta có ${y_0} =  \pm {{4\sqrt 3 } \over 7}.$

Vậy $A\left( {{2 \over 7};{{4\sqrt 3 } \over 7}} \right),B\left( {{2 \over 7}; - {{4\sqrt 3 } \over 7}} \right)$ hoặc $A\left( {{2 \over 7}; - {{4\sqrt 3 } \over 7}} \right),B\left( {{2 \over 7};{{4\sqrt 3 } \over 7}} \right)$

Giaibaitap.me