Bài 35 trang 66 SGK Hình học 10 nâng cao

Bài 35. Giải tam giác \(ABC\), biết

a) \(a = 14,\,\,b = 18,\,\,c = 20\);                                 

b) \(a = 6,\,\,b = 7,3,\,\,c = 4,8\);

c) \(a = 4,\,\,b = 5,\,\,c = 7\)

Hướng dẫn trả lời

a)  Áp dụng định lí cosin ta có

\(\eqalign{
& \cos A = {{{b^2} + {c^2} - {a^2}} \over {2bc}} = {{{{18}^2} + {{20}^2} - {{14}^2}} \over {2.18.20}} \approx 0,73 \cr
& \cos B = {{{a^2} + {c^2} - {b^2}} \over {2ac}} = {{{{14}^2} + {{20}^2} - {{18}^2}} \over {2.14.20}} \approx 0,49 \cr
& \Rightarrow \,\,\,\widehat A \approx {43^0}\,\,,\,\,\widehat B \approx {61^0}\,,\,\,\widehat C \approx {76^0}. \cr} \)

b) Áp dụng định lí cosin ta có

\(\eqalign{
& \cos A = {{{b^2} + {c^2} - {a^2}} \over {2bc}} = {{{{(7,3)}^2} + {{(4,8)}^2} - {6^2}} \over {2.(7,3).(4.8)}} \approx 0,58 \cr
& \cos B = {{{a^2} + {c^2} - {b^2}} \over {2ac}} = {{{6^2} + {{(4,8)}^2} - {{(7,3)}^2}} \over {2.6.(4,8)}} \approx 0,1 \cr
& \Rightarrow \,\,\,\widehat A \approx {55^0}\,\,,\,\,\widehat B \approx {85^0}\,,\,\,\widehat C \approx {40^0}. \cr} \)

c) Áp dụng định lí cosin ta có

\(\eqalign{
& \cos A = {{{b^2} + {c^2} - {a^2}} \over {2bc}} = {{{5^2} + {7^2} - {4^2}} \over {2.5.7}} \approx 0,83 \cr
& \cos B = {{{a^2} + {c^2} - {b^2}} \over {2ac}} = {{{4^2} + {7^2} - {5^2}} \over {2.4.7}} \approx 0,71 \cr
& \Rightarrow \,\,\,\widehat A \approx {34^0}\,\,,\,\,\widehat B \approx {44^0}\,,\,\,\widehat C \approx {102^0}. \cr} \)

Bài 36 trang 66 SGK Hình học 10 nâng cao

Bài 36. Biết hai lực cùng tác dụng vào một vật và tạo với nhau góc \({40^0}\). Cường độ của hai lực đó là \(3N\) và \(4N\). Tính cường độ của lực tổng hợp.

Hướng dẫn trả lời

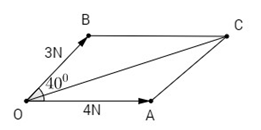
Theo quy tắc hình bình hành, ta vẽ hình bình hành \(AOBC\) thì \(\overrightarrow {OC}  = \overrightarrow {OA}  + \overrightarrow {OB} \).

Ta có \(\widehat {OBC} = {180^0} - {40^0} = {140^0}\) (Theo tính chất hình bình hành)

Áp dụng định lí cosin trong tam giác \(OBC\). Ta có

\(\eqalign{
& O{C^2} = O{B^2} + B{C^2} - 2OB.BC.\cos \widehat {OBC} \cr
& \,\,\,\,\,\,\,\,\,\,\, = {3^2} + {4^2} - 2.3.4.\cos {140^0} \approx 43,4 \cr
& \Rightarrow \,\,OC \approx 6,6 \cr} \)

Vậy cường độ của lực tổng  hợp là \(6,6N\).

Bài 37 trang 67 SGK Hình học 10 nâng cao

Bài 37. Từ vị trí \(A\) người  ta quan sát một cây cao (h.61)

Biết \(AH = 4\,m,\,HB = 20\,m,\,\widehat {BAC} = {45^0}\). Tính chiều cao của cây.

Hướng dẫn trả lời

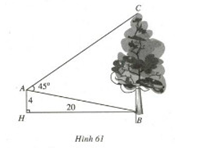
Tam giác \(AHB\) vuông tại \(H\) nên \(A{B^2} = A{H^2} + H{B^2} = {4^2} + {20^2} = 416\)

\(\eqalign{
& \Rightarrow AB \approx 20,4 \cr
& \tan \widehat {BAH} = {{HB} \over {HA}} = {{20} \over 4} = 5 \cr
& \Rightarrow \,\,\,\,\widehat {BAH} \approx 78,{7^0} \cr
& \Rightarrow \,\,\,\,\widehat {HAC} \approx 78,{7^0} + {45^0} \approx 123,{7^0} \cr}\)

\(\eqalign{
& \widehat {HAB} + \widehat {HBA} = {90^0} \cr
& \widehat {ABC} + \widehat {HBA} = {90^0} \cr
& \Rightarrow \widehat {HAB} = \widehat {ABC} \cr
& \Rightarrow \widehat {BCA} = {180^0} - \widehat {BAC} - \widehat {ABC} = {180^0} - \widehat {HAC} \cr} \)

  \(\Rightarrow \,\,\,\,\widehat {BCA} \approx {180^0} - 123,{7^0} = 56,{3^0}.\)

Ta có \({{BC} \over {{\mathop{\rm s}\nolimits} {\rm{in4}}{5^0}}} = {{AB} \over {{\mathop{\rm s}\nolimits} {\rm{in56,}}{{\rm{3}}^0}}}\)

 \(\Rightarrow \,\,BC = {{20,4} \over {{\mathop{\rm s}\nolimits} {\rm{in56,}}{{\rm{3}}^0}}}{\mathop{\rm s}\nolimits} {\rm{in4}}{5^0} \approx 17,4\)

Vậy cây cao \(17,4\) m.

Bài 38 trang 67 SGK Hình học 10 nâng cao

Bài 38. Trên nóc một tòa nhà có một cột ăng-ten cao \(5 m\). Từ vị trí quan sát \(A\) cao \(7 m\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và chân \(C\) của cột ăng-ten dưới góc \({50^0}\) và \({40^0}\) so với phương nằm ngang. Tính chiều cao của tòa nhà (h.62).

Hướng dẫn trả lời

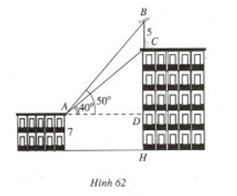
Đặt \(CD = x\), ta có

\(\eqalign{
& \tan {40^0} = {x \over {AD}}\,\,;\,\,\tan {50^0} = {BD\over {AD}} = {{x + 5} \over {AD}} \cr
& \Rightarrow \,\,{{x + 5} \over x} = {{\tan {{50}^0}} \over {\tan {{40}^0}}} \approx 1,42 \cr
& \Rightarrow \,\,0,42x = 5 \cr
& \Rightarrow \,\,x = 11,9 \cr} \)

Vậy chiều cao tòa nhà là \(HC = HD + DC = 7 + 11,9 = 18,9\) m.

Giaibaitap.me