Bài 1 trang 69 SGK Hình học 10 nâng cao

Bài 1. Chứng minh các công thức sau

a) \(\overrightarrow a .\,\overrightarrow b  = {1 \over 2}\left( {|\overrightarrow a {|^2} + |\overrightarrow b {|^2} - \overrightarrow {|a}  - \overrightarrow b {|^2}} \right)\);

b) \(\overrightarrow a .\,\overrightarrow b  = {1 \over 4}\left( {|\overrightarrow a  + \overrightarrow b {|^2} - |\overrightarrow a  - \overrightarrow b {|^2}} \right)\).

Hướng dẫn trả lời

a) Ta có \(|\overrightarrow a  - \overrightarrow b {|^2} = {(\overrightarrow a  - \overrightarrow b )^2} = |\overrightarrow a {|^2} - 2\overrightarrow a \overrightarrow b  + |\overrightarrow b {|^2}\)

 \( \Rightarrow \,\,\,\overrightarrow a .\,\overrightarrow b  = {1 \over 2}(|\overrightarrow a {|^2} + |\overrightarrow b {|^2} - |\overrightarrow a  - \overrightarrow b {|^2})\)

b) Ta có \(|\overrightarrow a  + \overrightarrow b {|^2} - |\overrightarrow a  - \overrightarrow b {|^2} = {(\overrightarrow a  + \overrightarrow b )^2} - {(\overrightarrow a  - \overrightarrow b )^2}\)           

\(\eqalign{
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = (\overrightarrow a + \overrightarrow b - \overrightarrow a + \overrightarrow b )(\overrightarrow a + \overrightarrow b + \overrightarrow a - \overrightarrow b ) = 4.\,\overrightarrow a .\,\overrightarrow b \cr
& \Rightarrow \,\,\overrightarrow a .\,\overrightarrow b = {1 \over 4}(|\overrightarrow a + \overrightarrow b {|^2} - |\overrightarrow a - \overrightarrow b {|^2}). \cr} \)

Bài 2 trang 69 SGK Hình học 10 nâng cao

Bài 2. Gọi \(G\) là trọng tâm tam giác \(ABC\).

a) Chứng minh rằng với mọi điểm \(M\), ta luôn có

\(M{A^2} + M{B^2} + M{C^2} = 3M{G^2} + G{A^2} + G{B^2} + G{C^2}\).

b) Tìm tập hợp các điểm \(M\) sao cho \(M{A^2} + M{B^2} + M{C^2} = {k^2}\), trong đó \(k\) là một số cho trước.

Hướng dẫn trả lời

Ta có

\(\eqalign{
& M{A^2} + M{B^2} + M{C^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + {\overrightarrow {MC} ^2} \cr
&= {(\overrightarrow {GA} - \overrightarrow {GM} )^2} + {(\overrightarrow {GB} - \overrightarrow {GM} )^2} + {(\overrightarrow {GC} - \overrightarrow {GM} )^2} \cr
&  = {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2} + 3{\overrightarrow {MG} ^2} - 2\overrightarrow {GM} (\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} ) \cr
&= 3M{G^2} + G{A^2} + G{B^2} + G{C^2} \cr} \)

b)  Áp dụng câu a), ta có

 \(M{A^2} + M{B^2} + M{C^2} = {k^2}\,\, \Leftrightarrow \,\,3M{G^2} = {k^2} - (G{A^2} + G{B^2} + G{C^2})\)

+) Nếu \({k^2} > G{A^2} + G{B^2} + G{C^2}\) thì tập hợp các điểm \(M\) là đường tròn tâm \(G\) bán kính \(\sqrt {{1 \over 3}\left[ {{k^2} - (G{A^2} + G{B^2} + G{C^2})} \right]} \).

+) Nếu \({k^2} = G{A^2} + G{B^2} + G{C^2}\) thì tập hợp các điểm \(M\) chỉ gồm một phần tử là \(G\).

+) Nếu \({k^2} < G{A^2} + G{B^2} + G{C^2}\) thì tập hợp điểm \(M\) là tập rỗng.

Bài 3 trang 70 SGK Hình học 10 nâng cao

Bài 3. Cho hình bình hành \(ABCD\). Tìm tập hợp các điểm \(M\) sao cho

\(M{A^2} + M{B^2} + M{C^2} + M{D^2} = {k^2}\), trong đó \(k\) là một số cho trước.

Hướng dẫn trả lời

Gọi \(O\) là tâm hình bình hành \(ABCD\), ta có

\(\eqalign{
& M{A^2} + M{B^2} + M{C^2} + M{D^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + {\overrightarrow {MC} ^2} + {\overrightarrow {MD} ^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {(\overrightarrow {OA} - \overrightarrow {OM} )^2} + {(\overrightarrow {OB} - \overrightarrow {OM} )^2} + {(\overrightarrow {OC} - \overrightarrow {OM} )^2} + {(\overrightarrow {OD} - \overrightarrow {OM} )^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = O{A^2} + O{B^2} + O{C^2} + O{D^2} + 4O{M^2} - 2\overrightarrow {OM} (\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} ) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2(O{A^2} + O{B^2}) + 4O{M^2} \cr} \)

Do đó \(M{A^2} + M{B^2} + M{C^2} + M{D^2} = {k^2}\,\, \Leftrightarrow \,\,\,4O{M^2} = {k^2} - 2(O{A^2} + O{B^2})\).

+) Nếu \({k^2} > 2(O{A^2} + O{B^2})\) thì tập hợp các điểm \(M\) là đường tròn tâm \(O\) bán kính \(\sqrt {{1 \over 4}\left[ {{k^2} - 2(O{A^2} + O{B^2})} \right]} \).

+) Nếu \({k^2} = 2(O{A^2} + O{B^2})\) thì tập hợp các điểm \(M\) chỉ gồm một phần tử là \(O\).

+) Nếu \({k^2} < 2(O{A^2} + O{B^2})\) thì tập hợp điểm \(M\) là tập rỗng.

Bài 4 trang 70 SGK Hình học 10 nâng cao

Trên hình 63 có vẽ hai tam giác vuông cân ABC và A'B'C' có chung đỉnh A. Gọi I và J lần lượt là trung điểm của hai đoạn thẳng BB' và CC'. Chứng minh rằng

a) \(AI \bot C{C'}\,,\,AJ \bot B{B'}\,\);

b) \(B{C'}\,\, \bot {B'}C\,\,\).

Giải

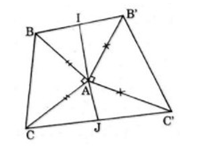
Ta có \(\overrightarrow {AI}  = {1 \over 2}(\overrightarrow {AB}  + \overrightarrow {A{B'}} )\,\,;\,\,\overrightarrow {AJ}  = {1 \over 2}(\overrightarrow {AC}  + \overrightarrow {A{C'}} )\)

\(\eqalign{
& \Rightarrow \,\,\overrightarrow {AI} .\,\overrightarrow {C{C'}} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {A{B'}} ).\,(\overrightarrow {A{C'}} - \overrightarrow {AC} ) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}(\overrightarrow {AB} .\,\overrightarrow {A{C'}} - \overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {A{B'}} .\,\overrightarrow {A{C'}} - \overrightarrow {A{B'}} .\,\overrightarrow {AC} ) \cr} \)

Vì \(AB \bot AC\,,\,\,A{B'} \bot A{C'}\,\) nên \(\overrightarrow {AB} .\,\overrightarrow {AC}  = \overrightarrow {A{B'}} .\,\overrightarrow {A{C'}}  = 0\)

Mặt khác

\(\eqalign{
& \overrightarrow {AB} .\,\overrightarrow {A{C'}} = AB.\,A{C'}.\cos \widehat {BA{C'}} \cr
& \overrightarrow {A{B'}} .\,\overrightarrow {AC} = A{B'}.\,AC.\cos \widehat {{B'}AC} \cr
& \Rightarrow \,\,\,\overrightarrow {AB} .\,\overrightarrow {A{C'}} = \overrightarrow {A{B'}} .\,\overrightarrow {AC} \,\, \Rightarrow \,\,\overrightarrow {AI} .\,\overrightarrow {C{C'}} = 0\,\, \Rightarrow \,\,AI \bot C{C'} \cr} \)

Tương tự \(\overrightarrow {AJ} .\,\overrightarrow {B{B'}}  = {1 \over 2}(\overrightarrow {AC}  + \overrightarrow {A{C'}} ).\,(\overrightarrow {A{B'}}  - \overrightarrow {AB} )\)

\(\eqalign{
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}(\overrightarrow {AC} .\,\overrightarrow {A{B'}} - \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {A{C'}} .\,\overrightarrow {A{B'}} - \overrightarrow {A{C'}} .\,\overrightarrow {AB} ) =0\cr
& \Rightarrow \,\,AJ \bot B{B'} \cr} \)

b) Ta có

\(\eqalign{
& \overrightarrow {B{C'}} .\,\overrightarrow {{B'}C} = (\overrightarrow {A{C'}} - \overrightarrow {AB} ).\,(\overrightarrow {AC} - \overrightarrow {A{B'}} ) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {A{C'}} .\,\overrightarrow {AC} - \overrightarrow {A{C'}} .\,\overrightarrow {A{B'}} - \overrightarrow {AB} .\,\overrightarrow {AC} + \overrightarrow {AB} .\,\overrightarrow {A{B'}} \cr} \)

 \(\overrightarrow {AB} .\,\overrightarrow {A{B'}}  = AB.A{B'}.\cos \widehat {BA{B'}}\)

\(\overrightarrow {AC} .\,\overrightarrow {A{C'}}  = AC.A{C'}.\cos ({180^0} - \widehat {BA{B'}}) \)

                    \(=  - \overrightarrow {AB} .\,\overrightarrow {A{B'}}.\)

Do đó: \(\overrightarrow {B{C'}} .\,\overrightarrow {{B'}C} =\overrightarrow 0\)

Vậy \(B{C'} \bot {B'}C\).

Giaibaitap.me