Bài 31 trang 66 SGK Hình học 10 nâng cao

Bài 31. Gọi \(S\) là diện tích và \(R\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\). Chứng minh rằng \(S = 2{R^2}\sin A\sin B\sin C\).

Hướng dẫn trả lời

Áp dụng công thức tính diện tích và định lí sin trong tam giác \(ABC\) .Ta có

\(\eqalign{
& S = {{abc} \over {4R}} = {{(2R\sin A).(2R\sin B).(2R\sin C)} \over {4R}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2{R^2}\sin A\sin B\sin C \cr} \)

Bài 32 trang 66 SGK Hình học 10 nâng cao

Bài 32. Chứng minh rằng diện tích của một tứ giác bằng nửa tích hai đường chéo và sin của góc hợp bởi hai đường chéo đó.

Hướng dẫn trả lời

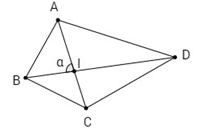
Gọi \(I\) là giao điểm của hai đường chéo \(AC, BD\) và \(\widehat {AIB} = \alpha \).

Ta có \({S_{ABI}} = {1 \over 2}AI.BI.\sin \alpha \,\,,\,\,\,{S_{ADI}} = {1 \over 2}AI.DI.\sin ({180^0} - \alpha ) = \,{1 \over 2}AI.DI.\sin \alpha \,\)

Suy ra \({S_{ABD}} = {S_{ABI}} + {S_{ADI}} = {1 \over 2}AI.(BI + DI).\sin \alpha  = {1 \over 2}AI.BD.\sin \alpha \)

Tương tự ta suy ra \({S_{BCD}} = {S_{BIC}} + {S_{CDI}} = {1 \over 2}CI.BD.\sin \alpha \)

Từ đó suy ra

\({S_{ABCD}} = {S_{ABD}} + {S_{BCD}} = {1 \over 2}.BD.(AI + CI).\sin \alpha  = {1 \over 2}.BD.AC.\sin \alpha. \)

Bài 33 trang 66 SGK Hình học 10 nâng cao

Bài 33. Giải tam giác \(ABC\), biết

a) \(c = 14,\,\widehat A = {60^0},\,\widehat B = {40^0}\);                                

b) \(b = 4,5,\,\widehat A = {30^0},\,\widehat C = {75^0}\);

c) \(c = 35,\,\widehat A = {40^0},\,\widehat C = {120^0}\);                              

d) \(a = 137,5;\;\widehat B = {83^0},\,\widehat C = {57^0}\).

Hướng dẫn trả lời

a)  Ta có \(\widehat C = {180^0} - {60^0} - {40^0} = {80^0}\)

Áp dụng định lí sin :  

\(\eqalign{
& \,\,\,\,\,\,{a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = {{14} \over {{\mathop{\rm s}\nolimits} {\rm{in8}}{{\rm{0}}^0}}}\,\,\,\, \Rightarrow \,\,a = {{14} \over {{\mathop{\rm s}\nolimits} {\rm{in8}}{{\rm{0}}^0}}}.\sin {60^0} \approx 12,3 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b = {{14} \over {{\mathop{\rm s}\nolimits} {\rm{in8}}{{\rm{0}}^0}}}.\sin {40^0} \approx 9,1 \cr} \)

b) Ta có \(\widehat B = {180^0} - {30^0} - {75^0} = {75^0}\)

Áp dụng định lí sin

\(\eqalign{
& \,\,\,\,\,\,{a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = {{4,5} \over {{\mathop{\rm s}\nolimits} {\rm{in7}}{{\rm{5}}^0}}}\,\,\, \Rightarrow \,\,a = {{4,5} \over {{\mathop{\rm s}\nolimits} {\rm{in7}}{{\rm{5}}^0}}}.\sin {30^0} \approx 2,3 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,c = {{4,5} \over {{\mathop{\rm s}\nolimits} {\rm{in7}}{{\rm{5}}^0}}}.\sin {75^0} = 4,5 \cr} \)

c)  Ta có \(\widehat B = {180^0} - {120^0} - {40^0} = {20^0}\)

Áp dụng định lí sin :

\(\eqalign{
& \,\,\,\,\,\,{a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = {{35} \over {{\mathop{\rm s}\nolimits} {\rm{in12}}{{\rm{0}}^0}}}\,\,\,\,\, \Rightarrow \,\,a = {{35} \over {{\mathop{\rm s}\nolimits} {\rm{in12}}{{\rm{0}}^0}}}.\sin {40^0} \approx 26 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b = {{35} \over {{\mathop{\rm s}\nolimits} {\rm{in12}}{{\rm{0}}^0}}}.\sin {20^0} \approx 13,8 \cr} \)

d)  Ta có \(\widehat A = {180^0} - {83^0} - {57^0} = {40^0}\)

Áp dụng định lí sin :

\(\eqalign{
& \,\,\,\,\,\,{a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}} = {{137,5} \over {{\mathop{\rm s}\nolimits} {\rm{in4}}{{\rm{0}}^0}}}\,\,\,\, \Rightarrow \,\,b = {{137,5} \over {{\mathop{\rm s}\nolimits} {\rm{in4}}{{\rm{0}}^0}}}.\sin {83^0} \approx 212,3 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,c = {{137,5} \over {{\mathop{\rm s}\nolimits} {\rm{in4}}{{\rm{0}}^0}}}.\sin {57^0} \approx 179,4 \cr} \)

Bài 34 trang 66 SGK Hình học 10 nâng cao

Bài 34. Giải tam giác \(ABC\), biết

a) \(a = 6,3,\,\,b = 6,3,\,\,\widehat C = {54^0}\);                            

b) \(b = 32,\,c = 45,\,\widehat A = {87^0}\);

c) \(a = 7,\,\,b = 23,\,\,\widehat C = {130^0}\).

Giải

a) \(ABC\) là tam giác cân tại \(C\) \( \Rightarrow \,\,\widehat A = \widehat B = {{{{180}^0} - {{54}^0}} \over 2} = {63^0}\). Áp dụng định lí sin ta có

 \(\,\,\,\,\,\,{a \over {\sin A}} = {c \over {\sin C}} = {{6,3} \over {{\mathop{\rm s}\nolimits} {\rm{in6}}{{\rm{3}}^0}}}\,\, \Rightarrow \,\,c = {{6,3} \over {{\mathop{\rm s}\nolimits} {\rm{in6}}{{\rm{3}}^0}}}.\sin {54^0} \approx 5,7\)

b)  Áp dụng định lí cosin ta có

\(\eqalign{
& {a^2} = {b^2} + {c^2} - 2bc.\cos A \cr
& \,\,\,\,\,\, = {32^2} + {45^2} - 2.32.45.\cos {87^0} \approx 2898,27 \cr
& \Rightarrow a \approx 53,8 \cr} \)

Áp dụng định lí sin ta có

\(\eqalign{
& \,\,\,\,\,\,{a \over {\sin A}} = {b \over {\sin B}}\,\, \Rightarrow \,\,\sin B = {{b\sin A} \over a} = {{32.\sin {{87}^0}} \over {53,8}} \approx 0,6 \cr
& \Rightarrow \,\,\widehat B \approx {36^0}\,,\,\,\widehat C \approx {57^0} \cr} \)

c)  Áp dụng định lí cosin ta có

\(\eqalign{
& {c^2} = {a^2} + {b^2} - 2ab.\cos C \cr
& \,\,\,\,\,\, = {7^2} + {23^2} - 2.7.23.\cos {130^0} \approx 785 \cr
& \Rightarrow c \approx 28 \cr
& \cos A = {{{b^2} + {c^2} - {a^2}} \over {2bc}} = {{{{23}^2} + {{28}^2} - {7^2}} \over {2.23.28}} \approx 0,98 \cr
& \Rightarrow \,\,\widehat A = {11^0}\,,\,\,\widehat B = {39^0} \cr} \)

Giaibaitap.me