Bài 2.17 trang 91 Sách bài tập (SBT) Toán Hình học 10

Tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 11 cm.

a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) và chứng tỏ rằng tam giác ABC có góc A tù.

b) Trên cạnh AB lấy điểm M sao cho AM = 2 cm và gọi N là trung điểm của cạnh AC. Tính \(\overrightarrow {AM} .\overrightarrow {AN} \).

Gợi ý làm bài

(h.2.21)

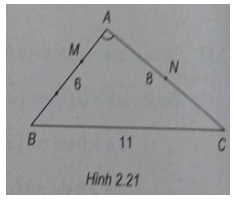
a) 

\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {AC} = {1 \over 2}(A{C^2} + A{B^2} - B{C^2}) \cr
& = {1 \over 2}({8^2} + {6^2} - {11^2}) = - {{21} \over 2} \cr} \)

\( = AB.AC.cosA =  - {{21} \over 2}\)

=> Góc A tù

b) Ta có:

\(\overrightarrow {AM}  = {1 \over 3}\overrightarrow {AB} ,\overrightarrow {AN}  = {1 \over 2}\overrightarrow {AC} \)

Do đó:

\(\eqalign{
& \overrightarrow {AM.} \overrightarrow {AN} = {1 \over 3}\overrightarrow {AB} .{1 \over 2}\overrightarrow {AC} \cr
& = {1 \over 6}\overrightarrow {AB} .\overrightarrow {AC} = {1 \over 6}.( - {{21} \over 2}) = - {7 \over 4} \cr}\)

Bài 2.18 trang 92 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC cân (AB = AC). Gọi H là trung điểm của cạnh BC, D là hình chiếu vuông góc của H trên cạnh AC, M là trung điểm của đoạn HD. Chứng minh rằng AM vuông góc với BD.

Gợi ý làm bài

(h.2.22) 

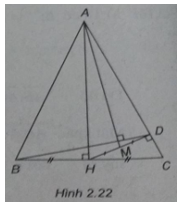
Ta cần chứng minh \(\overrightarrow {AM} .\overrightarrow {BD}  = 0\)

Tac có: \(2\overrightarrow {AM}  = \overrightarrow {AH}  + \overrightarrow {AD} \) vì M là trung điểm của đoạn HD.

\(\overrightarrow {BD}  = \overrightarrow {BH}  + \overrightarrow {HD} \)

Do đó:

\(2\overrightarrow {AM} .\overrightarrow {BD}  = (\overrightarrow {AH}  + \overrightarrow {AD} ).(\overrightarrow {BH}  + \overrightarrow {HD} )\)

\(= \underbrace {\overrightarrow {AH} .\overrightarrow {BH} }_{ = 0} + \overrightarrow {AH} .\overrightarrow {HD}  + \overrightarrow {AD} .\overrightarrow {BH}  + \underbrace {\overrightarrow {AD} .\overrightarrow {HD} }_{ = 0}\)

\( =  > \,2\overrightarrow {AM} .\overrightarrow {BD}  = \overrightarrow {AH} .\overrightarrow {HD}  + \overrightarrow {AD} .\overrightarrow {BH} \)

\( = (\overrightarrow {AH} .\overrightarrow {HD}  + (\overrightarrow {AH}  + \overrightarrow {HD} ).\overrightarrow {BH} \)

\( = \overrightarrow {AH} .\overrightarrow {HD}  + \underbrace {\overrightarrow {AH} .\overrightarrow {BH} }_{ = 0} + \overrightarrow {HD} .\overrightarrow {BH} \)

\( = \overrightarrow {HD} .(\underbrace {\overrightarrow {AH} .\overrightarrow {BH} }_{\overrightarrow {AC} }) = \overrightarrow {HD} .\overrightarrow {AC}  = 0\)

Vậy AM vuông góc với BD.

Bài 2.19 trang 92 Sách bài tập (SBT) Toán Hình học

Cho hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a  + \overrightarrow b } \right| = 13\). Tính tích vô hướng \(\overrightarrow a .(\overrightarrow a  + \overrightarrow b )\) và suy ra góc giữa hai vec tơ \(\overrightarrow a \) và \(\overrightarrow a  + \overrightarrow b \)

Gợi ý làm bài

(h.2.23)

Dựng tam giác ABC có AB = 5, BC= 12 và AC = 13.

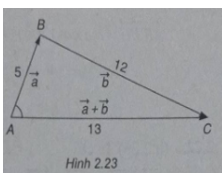
Ta có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a  + \overrightarrow b } \right| = 13\)

Và \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {BC}  = \overrightarrow b ,\overrightarrow {AC}  = \overrightarrow a  + \overrightarrow b \)

Khi đó \(\overrightarrow a (\overrightarrow a  + \overrightarrow b ) = \overrightarrow {AB} .\overrightarrow {AC} \)

Mặt khác ta có:

\(\overrightarrow {AB} .\overrightarrow {AC}  = {1 \over 2}(A{C^2} + A{B^2} - B{C^2})\)

\( = {1 \over 2}({13^2} + {5^2} - {12^2}) = 25\)

Ta suy ra:

\(\eqalign{
& \cos (\overrightarrow {AB} .\overrightarrow {AC} ) = {{\overrightarrow {AB} .\overrightarrow {AC} } \over {\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} \cr
& = {{25} \over {5.13}} \approx 0,3846 \cr} \)

Suy ra \((\overrightarrow {AB} .\overrightarrow {AC} ) \approx {67^0}23'\)

Bài 2.20 trang 92 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC. Gọi H là trực tâm của tam giác và M là trung điểm của cạnh BC. Chứng minh rằng \(\overrightarrow {MH} .\overrightarrow {MA}  = {1 \over 4}B{C^2}\)

Gợi ý làm bài

(h.2.24)

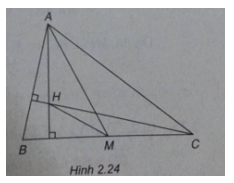
Ta có \(\overrightarrow {AM}  = {1 \over 2}(\overrightarrow {AB}  + \overrightarrow {AC} )\)

\(\overrightarrow {HM}  = {1 \over 2}(\overrightarrow {HB}  + \overrightarrow {HC} )\)

\( =  > \overrightarrow {AM} .\overrightarrow {HM}  = {1 \over 4}(\overrightarrow {AB}  + \overrightarrow {AC} ).(\overrightarrow {HB}  + \overrightarrow {HC} )\)

\( = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {HB}  + \underbrace {\overrightarrow {AB} .\overrightarrow {HC} }_{ = 0} + \underbrace {\overrightarrow {AC} \overrightarrow {.HB} }_{ = 0} + \overrightarrow {AC} .\overrightarrow {HC} )\)

\( = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {HB}  + \overrightarrow {AC} .\overrightarrow {HC} )\)

\( = {1 \over 4}\left[ {\overrightarrow {AB} .(\overrightarrow {HC}  + \overrightarrow {CB} ) + \overrightarrow {AC} .(\overrightarrow {HB}  + \overrightarrow {BC} )} \right]\)

\( = {1 \over 4}\left[ {\underbrace {\overrightarrow {AB} .\overrightarrow {HC} }_0 + \overrightarrow {AB} .\overrightarrow {CB}  + \underbrace {\overrightarrow {AC} .\overrightarrow {HB} }_0 + \overrightarrow {AC} .\overrightarrow {BC} } \right]\)

\( = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {CB}  + \overrightarrow {AC} .\overrightarrow {BC} ) = {1 \over 4}(\overrightarrow {AB} .\overrightarrow {CB}  - \overrightarrow {AC} .\overrightarrow {CB} )\)

\( = {1 \over 4}\overrightarrow {CB} .(\underbrace {\overrightarrow {AB}  - \overrightarrow {AC} }_{\overrightarrow {CB} }) = {1 \over 4}{\overrightarrow {CB} ^2} = {1 \over 4}{\overrightarrow {BC} ^2}\)

Giaibaitap.me