Bài 2.21 trang 92 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác đều ABC cạnh a. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) và \(\overrightarrow {AB} .\overrightarrow {BC} \)

Gợi ý làm bài

(H.2.25) 

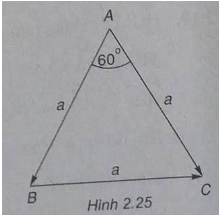
\(\overrightarrow {AB} .\overrightarrow {AC}  = a.a.\cos {60^0} = {1 \over 2}{a^2}\)

\(\overrightarrow {AB} .\overrightarrow {AC}  = a.a.\cos {120^0} =  - {1 \over 2}{a^2}\)

Bài 2.22 trang 92 Sách bài tập (SBT) Toán Hình học 10

Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau và cắt nhau tại M. Gọi P là trung điểm của cạnh AD. Chứng minh rằng MP vuông góc với BC khi và chỉ khi \(\overrightarrow {MA} .\overrightarrow {MC}  = \overrightarrow {MB} .\overrightarrow {MD} \)

Gợi ý làm bài

(h.2.26)

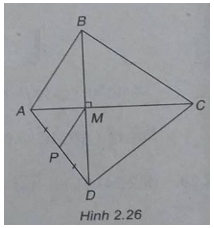
\(2\overrightarrow {MP} .\overrightarrow {BC}  = (\overrightarrow {MA}  + \overrightarrow {MD} )(\overrightarrow {MC}  - \overrightarrow {MB} )\)

\( = \overrightarrow {MA} .\overrightarrow {MC}  - \underbrace {\overrightarrow {MA} .\overrightarrow {MB} }_0 + \underbrace {\overrightarrow {MD} .\overrightarrow {MC} }_0 - \overrightarrow {MD} .\overrightarrow {MB} \)

\(= \overrightarrow {MA} .\overrightarrow {MC}  - \overrightarrow {MD} .\overrightarrow {MB} \)

Do đó: \(\overrightarrow {MP}  \bot \overrightarrow {BC}  \Leftrightarrow \overrightarrow {MP} .\overrightarrow {BC}  = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {MA} .\overrightarrow {MC}  = \overrightarrow {MD} .\overrightarrow {MB}\)

Bài 2.23 trang 92 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng Oxy cho tam giác ABC với A = (2;4), B = ( - 3;1) và C = (3;1). Tính:

a) Tọa độ điểm D để tứ giác ABCD là hình bình hành;

b) Tọa độ chân của đường cao vẽ từ đỉnh A.

Gợi ý làm bài

(h.2.27)

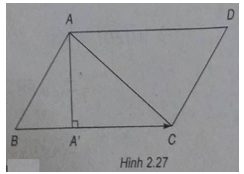
a) Vì ABCD là hình bình hành nên ta có:

\(\overrightarrow {BD}  = \overrightarrow {BA}  + \overrightarrow {BC} \) trong đó \(\overrightarrow {BA}  = (5;3)\)

\(\overrightarrow {BC}  = (6; - 2)\)

\( =  > \,\overrightarrow {BD}  = (11;1)\)

Giả sử D có tọa độ \(({x_D},{y_D})\)

Vì \(\overrightarrow {BD}  = (11;1)\) và B(-3; 1) nên ta có:

\(\left\{ \matrix{
{x_D} + 3 = 11 \hfill \cr
{y_D} - 1 = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_D} = 8 \hfill \cr
{y_D} = 2 \hfill \cr} \right.\)

Chú ý: Ta có thể dựa vào biểu thức vec tơ \(\overrightarrow {AD}  = \overrightarrow {BC} \) hoặc \(\overrightarrow {CD}  = \overrightarrow {BA} \) để tính tọa độ điểm D.

b) Gọi A(x;y) là chân đường cao vẽ từ A ta có:

\(\left\{ \matrix{
\overrightarrow {AA'} \bot \overrightarrow {BC} \,hay\overrightarrow {AA'} .\overrightarrow {BC} = 0 \hfill \cr
\overrightarrow {BA'} cung\,phuong\,voi\,\overrightarrow {BC} \hfill \cr} \right.\)

Với 

\(\eqalign{
& \overrightarrow {AA'} = (x - 2;y - 4), \cr
& \overrightarrow {BC} = (6; - 2), \cr
& \overrightarrow {BA'} = (x + 3;y - 1) \cr} \)

Do đó:

\(\left\{ \matrix{
(x - 2).6 + (y - 4).( - 2) = 0 \Leftrightarrow \overrightarrow {AA'} \bot \overrightarrow {BC} \hfill \cr
- 2(x + 3) = 6(y - 1) = 0 \Leftrightarrow \overrightarrow {BA'\,} cung\,phuong\,voi\,\overrightarrow {BC} \hfill \cr} \right.\)

\(\left\{ \matrix{
(x - 2).6 + (y - 4).( - 2) = 0 \Leftrightarrow \overrightarrow {AA'} \bot \overrightarrow {BC} \hfill \cr
- 2(x + 3) = 6(y - 1) = 0 \Leftrightarrow \overrightarrow {BA'} cung\,phuong\,voi\,\overrightarrow {BC} \hfill \cr} \right.\)

\(\eqalign{
& \Leftrightarrow \left\{ \matrix{
6x - 12 - 2y + 8 = 0 \hfill \cr
- 2x - 6 - 6y + 6 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
6x - 2y - 4 = 0 \hfill \cr
- 2x - 6y = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_{A'}} = {3 \over 5} \hfill \cr
{y_{A'}} = - {1 \over 5} \hfill \cr} \right. \cr} $\)

Bài 2.24 trang 92 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng Oxy, cho tam giác ABC có A=( - 1;1), B=(1;3) và C=(1;-1)

Chứng minh tam giác ABC là tam giác vuông cân tại A.

Gợi ý làm bài

Ta có: \(\overrightarrow {AB}  = (2;2),\overrightarrow {AC}  = (2; - 2)\). Do đó:

\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {AC} = 2.2 + 2.( - 2) = 0 \cr
& = > \overrightarrow {AB} \bot \overrightarrow {AC} \cr} \)

Mặt khác \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right| = \sqrt {4 + 4}  = 2\sqrt 2 \)

Vậy tam giác ABC vuông cân tại A.

Giaibaitap.me