Bài 2.13 trang 91 Sách bài tập (SBT) Toán Hình học 10

Cho hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \)  đều khác \(\overrightarrow 0 \). Tích vô hướng \(\overrightarrow a .\overrightarrow b \) khi nào dương, khi nào âm và  khi nào bằng 0?

Gợi ý làm bài

Tac có:

\(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos (\overrightarrow a ,\overrightarrow b )\)

Do đó:

\(\overrightarrow a .\overrightarrow b  > 0\) khi \(\cos (\overrightarrow a ,\overrightarrow b ) > 0\) nghĩa là \(0 \le (\overrightarrow a ,\overrightarrow b ) \le {90^0}\)

\(\overrightarrow a .\overrightarrow b  < 0\) khi \(\cos (\overrightarrow a ,\overrightarrow b ) < 0\) nghĩa là \({90^0} \le (\overrightarrow a ,\overrightarrow b ) \le {180^0}\)

\(\overrightarrow a .\overrightarrow b  = 0\) khi \(\cos (\overrightarrow a ,\overrightarrow b ) = 0\) nghĩa là \((\overrightarrow a ,\overrightarrow b ) = {90^0}\)

Bài 2.14 trang 91 Sách bài tập (SBT) Toán Hình học 10

Áp dụng tính chất giao hoán và tính chất phân phối của tích vô hướng hãy chứng minh các kết quả sau đây:

\({(\overrightarrow a  + \overrightarrow b )^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b \)

\({(\overrightarrow a  - \overrightarrow b )^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} - 2\overrightarrow a .\overrightarrow b \)

\((\overrightarrow a  + \overrightarrow b )(\overrightarrow a  - \overrightarrow b ) = {\left| {\overrightarrow a } \right|^2} - {\left| {\overrightarrow b } \right|^2}\)

Gợi ý làm bài

\(\eqalign{
& {(\overrightarrow a + \overrightarrow b )^2} = (\overrightarrow a + \overrightarrow b ).(\overrightarrow a + \overrightarrow b ) \cr
& = \overrightarrow a .\overrightarrow a + \overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow a + \overrightarrow b .\overrightarrow b \cr} \)

\(= {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b \)

Các tính chất còn lại được chứng minh tương tự.

Bài 2.15 trang 91 Sách bài tập (SBT) Toán Hình học 10

Tam giác ABC vuông tại A và có  AB = AC = a. Tính:

a) \(\overrightarrow {AB} .\overrightarrow {AC} \)

b) \(\overrightarrow {BA} .\overrightarrow {BC} \)

c) \(\overrightarrow {AB} .\overrightarrow {BC} \)

Gợi ý làm bài

(h2.20)

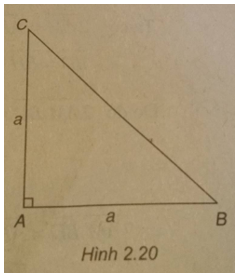
\(\overrightarrow {AB} .\overrightarrow {AC}  = 0\)

\(\overrightarrow {BA} .\overrightarrow {BC}  = a.a\sqrt 2 .\cos {45^0} = {a^2}\)

\(\overrightarrow {AB} .\overrightarrow {BC}  = a.a\sqrt 2 .\cos {135^0} =  - {a^2}\)

Bài 2.16 trang 91 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC có AB = 5 cm, BC = 7 cm, CA = 8 cm.

a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) rồi suy ra giá trị của góc A;

b) Tính \(\overrightarrow {CA} .\overrightarrow {CB} \)

Gợi ý làm bài

a) Ta có:

\(B{C^2} = {\overrightarrow {BC} ^2} = {(\overrightarrow {AC}  - \overrightarrow {AB} )^2}\)

\({\overrightarrow { = AC} ^2} + {\overrightarrow {AB} ^2} - 2\overrightarrow {AC} .\overrightarrow {AB} \)

Do đó:

\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {AC} = {{{{\overrightarrow {AC} }^2} + {{\overrightarrow {AB} }^2} - {{\overrightarrow {BC} }^2}} \over 2} \cr
& = {{{8^2} + {5^2} - {7^2}} \over 2} = 20 \cr} \)

Mặt khác:

\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.cosA \cr
& = 5.8.cosA = 20 \cr} \)

Suy ra \(\cos A = {{20} \over {40}} = {1 \over 2} =  > \widehat A = {60^0}\)

b) Ta có:

\(\eqalign{
& B{A^2} = {\overrightarrow {BA} ^2} = {(\overrightarrow {CA} - \overrightarrow {CB} )^2} \cr
& = {\overrightarrow {CA} ^2} + {\overrightarrow {CB} ^2} - 2\overrightarrow {CA} .\overrightarrow {CB} \cr} \)

Do đó:

\(\eqalign{
& \overrightarrow {CA} .\overrightarrow {CB} = {1 \over 2}({\overrightarrow {CA} ^2} + {\overrightarrow {CB} ^2} - {\overrightarrow {BA} ^2}) \cr
& = {1 \over 2}({8^2} + {7^2} - {5^2}) = 44 \cr} \)

Giaibaitap.me