Bài 19 trang 194 Sách bài tập (SBT) Toán Đại số 10

Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc \(\alpha ,\beta \)

a) \(\sin 6\alpha \cot 3\alpha  - c{\rm{os6}}\alpha \)

b) \({{\rm{[}}\tan ({90^0} - \alpha ) - \cot ({90^0} + \alpha ){\rm{]}}^2} - {{\rm{[}}c{\rm{ot(18}}{{\rm{0}}^0} + \alpha ) + \cot ({270^0} + \alpha ){\rm{]}}^2}\)

c) \((\tan \alpha  - \tan \beta )cot(\alpha  - \beta ) - \tan \alpha \tan \beta \)

d) \((\cot {\alpha  \over 3} - \tan {\alpha  \over 3})\tan {{2\alpha } \over 3}\)

Gợi ý làm bài

a) 

\(\eqalign{
& \sin 6\alpha \cot 3\alpha - c{\rm{os6}}\alpha \cr
& = 2\sin 3\alpha \cos 3\alpha .{{\cos 3\alpha } \over {\sin 3\alpha }} - (2{\cos ^2}3\alpha - 1) \cr} \)

= \(2{\cos ^2}3\alpha  - 2{\cos ^2}3\alpha  + 1 = 1\)

b) 

\({{\rm{[}}\tan ({90^0} - \alpha ) - \cot ({90^0} + \alpha ){\rm{]}}^2} - {{\rm{[}}c{\rm{ot(18}}{{\rm{0}}^0} + \alpha ) + \cot ({270^0} + \alpha ){\rm{]}}^2}\)

= \({(\cot \alpha  + \tan \alpha )^2} - {(\cot \alpha  - \tan \alpha )^2}\)

= \({\cot ^2}\alpha  + 2 + {\tan ^2}\alpha  - {\cot ^2}\alpha  + 2 - {\tan ^2}\alpha  = 4\)

c)

\(\eqalign{
& (\tan \alpha - \tan \beta )cot(\alpha - \beta ) - \tan \alpha \tan \beta \cr
& = {{\tan \alpha - \tan \beta } \over {\tan (\alpha - \beta )}} - \tan \alpha \tan \beta \cr} \)

=\(1 + \tan \alpha \tan \beta  - \tan \alpha \tan \beta  = 1\)

d) 

\(\eqalign{
& (\cot {\alpha \over 3} - \tan {\alpha \over 3})\tan {{2\alpha } \over 3} \cr
& = ({{\cos {\alpha \over 3}} \over {\sin {\alpha \over 3}}} - {{\sin {\alpha \over 3}} \over {\cos {\alpha \over 3}}}){{\sin {{2\alpha } \over 3}} \over {\cos {{2\alpha } \over 3}}} \cr} \)

= \(\eqalign{
& {{{{\cos }^2}{\alpha \over 3} - {{\sin }^2}{\alpha \over 3}} \over {\sin {\alpha \over 3}\cos {\alpha \over 3}}}.{{\sin {{2\alpha } \over 3}} \over {\cos {{2\alpha } \over 3}}} \cr
& = {{\cos {{2\alpha } \over 3}} \over {{1 \over 2}\sin {{2\alpha } \over 3}}}.{{\sin {{2\alpha } \over 3}} \over {\cos {{2\alpha } \over 3}}} = 2 \cr} \)

Bài 20 trang 194 Sách bài tập (SBT) Toán Đại số 10

Không sử dụng bảng số và máy tính, hãy tính

a) \({\sin ^4}{\pi  \over {16}} + {\sin ^4}{{3\pi } \over {16}} + {\sin ^4}{{5\pi } \over {16}} + {\sin ^4}{{7\pi } \over {16}}\)

b) \(\cot 7,{5^0} + \tan 67,{5^0} - \tan 7,{5^0} - \cot 67,{5^0}\)

Gợi ý làm bài

a) \({\sin ^4}{\pi  \over {16}} + {\sin ^4}{{3\pi } \over {16}} + {\sin ^4}{{5\pi } \over {16}} + {\sin ^4}{{7\pi } \over {16}}\)

\( = {\left( {{{1 - \cos {\pi  \over 8}} \over 2}} \right)^2} + {\left( {{{1 - \cos {{3\pi } \over 8}} \over 2}} \right)^2} + {\left( {{{1 - \cos {{5\pi } \over 8}} \over 2}} \right)^2} + {\left( {{{1 - \cos {{7\pi } \over 8}} \over 2}} \right)^2}\)

\( = {1 \over 4}\left( {1 - 2\cos {\pi  \over 8} + {{\cos }^2}{\pi  \over 8} + 1 - 2\cos {{3\pi } \over 8} + {{\cos }^2}{{3\pi } \over 8} + 1 - 2\cos {{5\pi } \over 8} + {{\cos }^2}{{5\pi } \over 8} + 1 - 2\cos {{7\pi } \over 8} + {{\cos }^2}{{7\pi } \over 8}} \right)\)

\( = 1 - {1 \over 2}\left( {\cos {\pi  \over 8} + \cos {{3\pi } \over 8} + \cos {{5\pi } \over 8} + \cos {{7\pi } \over 8}} \right) + {1 \over 4}\left( {{{1 + \cos {\pi  \over 4}} \over 2} + {{1 + \cos {{3\pi } \over 4}} \over 2} + {{1 + \cos {{5\pi } \over 4}} \over 2} + {{1 + \cos {{7\pi } \over 4}} \over 2}} \right)$\)

=\(1 - {1 \over 2}\left( {\cos {\pi  \over 8} + \cos {{3\pi } \over 8} - \cos {{3\pi } \over 8} - \cos {\pi  \over 8}} \right) + {1 \over 8}\left( {4 + {{\sqrt 2 } \over 2} - {{\sqrt 2 } \over 2} - {{\sqrt 2 } \over 2} + {{\sqrt 2 } \over 2}} \right)\)

= \({3 \over 2}\)

b) \(\cot 7,{5^0} + \tan 67,{5^0} - \tan 7,{5^0} - \cot 67,{5^0}\)

= \({{\cos 7,{5^0}} \over {\sin 7,{5^0}}} - {{\sin 7,{5^0}} \over {\cos 7,{5^0}}} + {{\sin 67,{5^0}} \over {\cos 67,{5^0}}} - {{\cos 67,{5^0}} \over {\sin 67,{5^0}}}\)

= \({{{{\cos }^2}7,{5^0} - {{\sin }^2}7,{5^0}} \over {\sin 7,{5^0}\cos 7,{5^0}}} + {{{{\sin }^2}67,{5^0} - {{\cos }^2}67,{5^0}} \over {sin67,{5^0}\cos 67,{5^0}}}\)

= \(\eqalign{
& {{\cos {{15}^0}} \over {{1 \over 2}\sin {{15}^0}}} - {{\cos {{135}^0}} \over {{1 \over 2}\sin {{135}^0}}} \cr
& = {{2(\sin {{135}^0}\cos {{15}^0} - \cos {{135}^0}\sin {{15}^0})} \over {\sin {{15}^0}\sin {{135}^0}}} \cr} \)

= \({{\sin ({{135}^0} - {{15}^0})} \over {\sin ({{45}^0} - {{30}^0})\sin ({{180}^0} - {{45}^0})}}\)

= \({{2\sin {{120}^0}} \over {(\sin {{45}^0}\cos {{30}^0} - \cos {{45}^0}\sin {{30}^0})sin{{45}^0}}}\)

\(\eqalign{
& = {{\sqrt 3 } \over {{{\sqrt 2 } \over 2}({{\sqrt 3 } \over 2} - {1 \over 2}).{{\sqrt 2 } \over 2}}} \cr
& = {{4\sqrt 3 } \over {\sqrt 3 - 1}} = 6 + 2\sqrt 3 \cr} $\)

Bài 21 trang 194 Sách bài tập (SBT) Toán Đại số 10

Rút gọn các biểu thức

a) \({{\sin 2\alpha  + \sin \alpha } \over {1 + c{\rm{os2}}\alpha {\rm{ + cos}}\alpha }}\)

b) \({{4{{\sin }^2}\alpha } \over {1 - c{\rm{o}}{{\rm{s}}^2}{\alpha  \over 2}}}\)

c) \({{1 + c{\rm{os}}\alpha  - \sin \alpha } \over {1 - c{\rm{os}}\alpha  - {\rm{sin}}\alpha }}\)

d) \({{1 + \sin \alpha  - 2{{\sin }^2}({{45}^0} - {\alpha  \over 2})} \over {4c{\rm{os}}{\alpha  \over 2}}}\)

Gợi ý làm bài

a) \({{\sin 2\alpha  + \sin \alpha } \over {1 + c{\rm{os2}}\alpha {\rm{ + cos}}\alpha }} = {{\sin \alpha (2\cos \alpha  + 1)} \over {2c{\rm{o}}{{\rm{s}}^2}\alpha {\rm{ + cos}}\alpha }}\)

= \({{\sin \alpha (2\cos \alpha  + 1)} \over {c{\rm{os}}\alpha (2{\rm{cos}}\alpha  + 1)}} = \tan \alpha \)

b) \({{4{{\sin }^2}\alpha } \over {1 - c{\rm{o}}{{\rm{s}}^2}{\alpha  \over 2}}} = {{16{{\sin }^2}{\alpha  \over 2}{{\cos }^2}{\alpha  \over 2}} \over {{{\sin }^2}{\alpha  \over 2}}} = 16{\cos ^2}{\alpha  \over 2}\)

c) \({{1 + c{\rm{os}}\alpha  - \sin \alpha } \over {1 - c{\rm{os}}\alpha  - {\rm{sin}}\alpha }} = {{2{{\cos }^2}{\alpha  \over 2} - 2\sin {\alpha  \over 2}\cos {\alpha  \over 2}} \over {2si{n^2}{\alpha  \over 2} - 2\sin {\alpha  \over 2}\cos {\alpha  \over 2}}}\)

= \({{2\cos {\alpha  \over 2}(\cos {\alpha  \over 2} - \sin {\alpha  \over 2})} \over {2\sin {\alpha  \over 2}(sin{\alpha  \over 2} - \cos {\alpha  \over 2})}} =  - \cot {\alpha  \over 2}\)

d) \({{1 + \sin \alpha  - 2{{\sin }^2}({{45}^0} - {\alpha  \over 2})} \over {4c{\rm{os}}{\alpha  \over 2}}} = {{\sin \alpha  + \cos ({{90}^0} - \alpha )} \over {4\cos {\alpha  \over 2}}}\)

=\({{\sin \alpha  + \sin \alpha } \over {4\cos {\alpha  \over 2}}} = {{4\sin {\alpha  \over 2}\cos {\alpha  \over 2}} \over {4\cos {\alpha  \over 2}}} = \sin {\alpha  \over 2}\)

Bài 22 trang 194 Sách bài tập (SBT) Toán Đại số 10

Cho hình thang cân ABCD có đáy nhỏ AB = AD. Biết \(\tan \widehat {BDC} = {3 \over 4}\) tính các giá trị lượng giác của \(\widehat {BAD}\)

Gợi ý làm bài

Ta có (h.64)

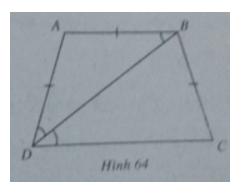
\(\widehat {ABD} = \widehat {ADB}\)

\(\widehat {ABD} = \widehat {BDC}\)

=> \(\widehat {BDC} = \widehat {ADB}\)

Suy ra \(\widehat {BAD} = \pi  - 2\widehat {BDC}\)

Từ đó ta có:

\(\eqalign{
& \tan \widehat {BAD} = - \tan 2\widehat {BDC} = - {{2\tan \widehat {BDC}} \over {1 - {{\tan }^2}\widehat {BDC}}} \cr
& = - {{2.{3 \over 4}} \over {1 - {9 \over {16}}}} = - {3 \over 2}.{{16} \over 7} = - {{24} \over 7} \cr} \)

Vì \({\pi  \over 2} < \widehat {BAD} < \pi \) nên \(\cos \widehat {BAD} < 0\). Do đó

\(\eqalign{
& \cos \widehat {BAD} = - {1 \over {\sqrt {1 + {{\tan }^2}\widehat {BAD}} }} \cr
& = - {1 \over {\sqrt {1 + {{576} \over {49}}} }} = - {7 \over {25}} \cr} \)

\(\eqalign{
& \sin \widehat {BAD} = \cos \widehat {BAD}.\tan \widehat {BAD} \cr
& = {{ - 7} \over {25}}.{{ - 24} \over 7} = {{24} \over {25}} \cr} \)

Giaibaitap.me