Bài 1.58 trang 46 Sách bài tập (SBT) Toán Hình học 10
Cho hình vuông ABCD, E là trung điểm của CD. Hãy phân tích theo hai vec tơ \(\overrightarrow u = \overrightarrow {AD} ,\overrightarrow v = \overrightarrow {AB} \).
Gợi ý làm bài
(h.1.70)
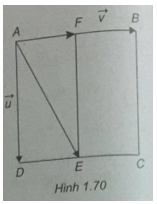
Gọi F là trung điểm của cạnh AB. Ta có
\(\overrightarrow {AE} = \overrightarrow {AD} + \overrightarrow {AF} = \overrightarrow u + {1 \over 2}\overrightarrow v \)
Vậy \(\overrightarrow {AE} = \overrightarrow u + {1 \over 2}\overrightarrow v\)
Bài 1.59 trang 46 Sách bài tập (SBT) Toán Hình học 10
Cho các điểm A, B, C trên trục \((O;\overrightarrow e )\) có tọa độ lần lượt là \(5; - 3; - 4\). Tính độ dài đại số của \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AC} ,\overrightarrow {BC} \)
Gợi ý làm bài
\(\eqalign{
& \overrightarrow {AB} = - 8,\overrightarrow {BA} = 8, \cr
& \overrightarrow {AC} = - 9,\overrightarrow {BC} = - 1 \cr} \)
Bài 1.60 trang 46 Sách bài tập (SBT) Toán Hình học 10
Cho hình thoi ABCD tâm O có AC = 8, BD = 6. Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\) sao cho \(\overrightarrow i \) và \(\overrightarrow {OC} \) cùng hướng, \(\overrightarrow j \) và \(\overrightarrow {OB} \) cùng hướng
a) Tìm tọa độ các đỉnh của hình thoi;
b) Tìm tọa độ trung điểm I của BC và trọng tâm của tam giác ABC;
c) Tìm tọa độ điểm đối xứng I' của I qua tâm O. Chứng minh A, I', D thẳng hàng
d) Tìm tọa độ của vec tơ \(\overrightarrow {AC} ,\overrightarrow {BD} ,\overrightarrow {BC} \)
Gợi ý làm bài
(Xem h.1.71)
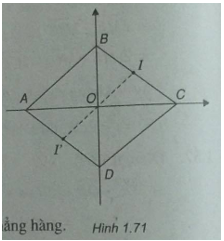
a) Ta có: AO = OC = 4 và OB = OD = 3
\( \Rightarrow A( - 4;0),C(4,0),B(0;3),D(0; - 3)\)
b) I là trung điểm BC \( \Rightarrow I\left( {2;{3 \over 2}} \right)\)
G là trọng tâm tam giác ABC \( \Rightarrow G(0;1)\)
c) I' đối xứng với I qua O \( \Rightarrow I'\left( { - 2; - {2 \over 3}} \right)\)
Ta có \(\overrightarrow {AI'} \left( {2; - {3 \over 2}} \right),\overrightarrow {AD} \left( {4; - 3} \right)\)
Vậy \(\overrightarrow {AD} = 2\overrightarrow {AI'} \)
Vậy A, I', D thẳng hàng
d) \(\overrightarrow {AC} (8;0),{\rm{ }}\overrightarrow {BD} (0; - 6),{\rm{ }}\overrightarrow {BC} (4; - 3){\rm{ }}\)
Giaibaitap.me
Giải bài tập trang 46 bài đề toán tổng hợp chương I Sách bài tập (SBT) Toán Hình học 10. Câu 1.61: Cho các điểm A'(-4;1), B'(2;4) và C'(2; - 2) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC...
Giải bài tập trang 47 bài đề toán tổng hợp chương I Sách bài tập (SBT) Toán Hình học 10. Câu 1.65: Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA...
Giải bài tập trang 47, 48 bài đề toán tổng hợp chương I Sách bài tập (SBT) Toán Hình học 10. Câu 1.69: Xét xem ba điểm sau có thẳng hàng không?...
Giải đề kiểm tra trang 48 chương I phần hình học Sách bài tập (SBT) Toán Hình học 10. Câu 1: Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Hãy thực hiện các phép toán sau...
