Bài 1.65 trang 47 Sách bài tập (SBT) Toán Hình học 10

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Gợi ý làm bài

Gọi G và G' lần lượt là trọng tâm các tam giác MPR và NQS. Ta có:

\(\eqalign{
& \overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GR} \cr
& = {1 \over 2}(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} + \overrightarrow {GE} + \overrightarrow {GF} ) \cr
& = \overrightarrow 0 \cr} \)

\(\eqalign{
& \overrightarrow {G'N} + \overrightarrow {G'Q} + \overrightarrow {G'S} \cr
& = {1 \over 2}(\overrightarrow {G'B} + \overrightarrow {G'C} + \overrightarrow {G'D} + \overrightarrow {G'E} + \overrightarrow {G'F} + \overrightarrow {G'A} ) \cr
& = \overrightarrow 0 \cr} \)

Do đó:

\(\eqalign{
& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} + \overrightarrow {GE} + \overrightarrow {GF} \cr
& = \overrightarrow {G'B} + \overrightarrow {G'C} + \overrightarrow {G'D} + \overrightarrow {G'E} + \overrightarrow {G'F} + \overrightarrow {G'A} \cr} \)

\( =  > 6\overrightarrow {GG'}  = \overrightarrow 0  =  > G \equiv G'\)

Bài 1.66 trang 47 Sách bài tập (SBT) Toán Hình học 10

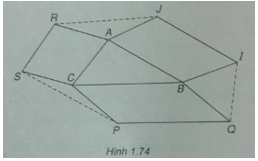
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng:

\(\overrightarrow {RJ}  + \overrightarrow {IQ}  + \overrightarrow {PS}  = \overrightarrow 0 \)

Gợi ý làm bài

(Xem hình 1.74)

\(\eqalign{
& \overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} \cr
& = \overrightarrow {RA} + \overrightarrow {AJ} + \overrightarrow {IB} + \overrightarrow {BQ} + \overrightarrow {PC} + \overrightarrow {CS} \cr} \)

\(= (\overrightarrow {RA}  + \overrightarrow {CS} ) + (\overrightarrow {AJ}  + \overrightarrow {IB} ) + (\overrightarrow {BQ}  + \overrightarrow {PC} )\)

\(= \overrightarrow 0 \)

Bài 1.67 trang 47 Sách bài tập (SBT) Toán Hình học 10

Cho ba lực \(\overrightarrow {{F_1}}  = \overrightarrow {MA} ,\overrightarrow {{F_2}}  = \overrightarrow {MB} \) và \(\overrightarrow {{F_3}}  = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_12}}\) đều là 100 N và  \(\widehat {AMB} = {60^0}\)

a) Đặt \(\overrightarrow {ME}  = \overrightarrow {MA}  + \overrightarrow {MB} \). Tính độ dài của đoạn ME

b) Tìm cường độ và hướng của lực \(\overrightarrow {{F_3}} \)

Gợi ý làm bài

(Xem hình 1.75)

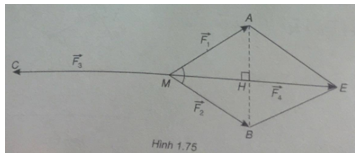
a) Vật đứng yên là do \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  = \overrightarrow 0 \)

Vẽ hình thoi MAEB ta có: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  = \overrightarrow {ME} \)

Tam giác MAB là tam giác đều có đường cao \(MH = {{100\sqrt 3 } \over 2}\)

Suy ra \(ME = 100\sqrt 3 \)

b) Lực \(\overrightarrow {{F_4}}  = \overrightarrow {ME}\) có cường độ là \(100\sqrt 3 N\)

Ta có \(\overrightarrow {{F_4}}  + \overrightarrow {{F_3}}  = \overrightarrow 0 \), do đó \(\overrightarrow {{F_3}} \) là vec tơ đối của \(\overrightarrow {{F_4}} \). Như vậy \(\overrightarrow {{F_3}} \) có cường độ là \(100\sqrt 3 N\) và ngược hướng với vec tơ \(\overrightarrow {ME} \)

Bài 1.68 trang 47 Sách bài tập (SBT) Toán Hình học 10

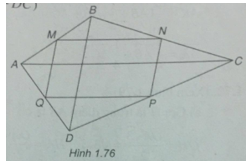
Cho tứ giác ABCD.Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh rằng:

a) \(\overrightarrow {MN}  = \overrightarrow {QP}\)

b) \(\overrightarrow {MP}  = \overrightarrow {MN}  + \overrightarrow {MQ} \)

Gợi ý làm bài

(Xem hình 1.76)

a) Ta có:

\(\overrightarrow {MN}  = \overrightarrow {MB}  + \overrightarrow {BN}  = {1 \over 2}(\overrightarrow {AB}  + \overrightarrow {BC} ) = {1 \over 2}\overrightarrow {AC} \)

\(\overrightarrow {QP}  = \overrightarrow {QD}  + \overrightarrow {DP}  = {1 \over 2}(\overrightarrow {AD}  + \overrightarrow {DC} ) = {1 \over 2}\overrightarrow {AC} \)

Suy ra \(\overrightarrow {MN}  = \overrightarrow {QP}\)

b) Tứ giác MNPQ có:  \(\left\{ \matrix{
MN{\rm{//}}QD \hfill \cr
MN = QP \hfill \cr} \right.\)

Suy ra MNPQ là hình bình hành.

Suy ra \(\overrightarrow {MP}  = \overrightarrow {MN}  + \overrightarrow {MQ} \)

Giaibaitap.me