Bài 1.69 trang 47 Sách bài tập (SBT) Toán Hình học 10

Xét xem ba điểm sau có thẳng hàng không?

a) A(2; - 3), B(5;1) và C(8; 5);

b) M(1;2), N(3; 6) và P(4;5).

Gợi ý làm bài

a) Ta có \(\overrightarrow {AB}  = (3;4),\overrightarrow {AC}  = (6;8),\overrightarrow {AC}  = 2\overrightarrow {AB} \)

=>A, B, C thẳng hàng.

b) \(\overrightarrow {MN}  = (2;4);\overrightarrow {MP}  = (3;3)\) mà \({2 \over 3} \ne {4 \over 3}\)

Vậy M, N, P không thẳng hàng.

Bài 1.70 trang 47 Sách bài tập (SBT) Toán Hình học 10

Cho hình chữ nhật ABCD. Gọi I là giao điểm của hai đường chéo AC và BD.

a) Với điểm M tùy ý, hãy chứng minh:

\(\overrightarrow {MA}  + \overrightarrow {MC}  = \overrightarrow {MB}  + \overrightarrow {MD} \)

b) Chứng minh rằng: \(\left| {\overrightarrow {AB}  + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB}  - \overrightarrow {AD} } \right|\)

Gợi ý làm bài

(Xem hình 1.77)

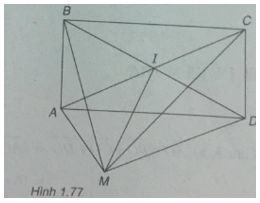
a) \(\overrightarrow {MA}  + \overrightarrow {MC}  = 2\overrightarrow {MI} \)

\(\overrightarrow {MB}  + \overrightarrow {MD}  = 2\overrightarrow {MI}\)

Vậy \(\overrightarrow {MA}  + \overrightarrow {MC}  = \overrightarrow {MB}  + \overrightarrow {MD} \)

b) \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC}  =  > \left| {\overrightarrow {AB}  + \overrightarrow {AD} } \right| = AC\)

\(\overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB}  =  > \left| {\overrightarrow {AB}  - \overrightarrow {AD} } \right| = DB\)

Vì hai đường chéo của hình chữ nhật dài bằng nhau nên

\(\left| {\overrightarrow {AB}  + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB}  - \overrightarrow {AD} } \right|\)

Bài 1.71 trang 48 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC. Gọi I là trung điểm của BC, K là trung điểm của BI.

Chứng minh rằng:

a) \(\overrightarrow {AK}  = {1 \over 2}\overrightarrow {AB}  + {1 \over 2}\overrightarrow {AI} \)

b) \(\overrightarrow {AK}  = {3 \over 4}\overrightarrow {AB}  + {1 \over 4}\overrightarrow {AC} \)

Gợi ý làm bài

(Xem hình 1.78)

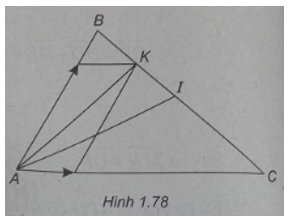
a) Vì K là trung điểm của BI nên \(\overrightarrow {AK}  = {1 \over 2}(\overrightarrow {AB}  + \overrightarrow {AI} )\) (1)

b) Vì I là trung điểm của BC nên \(\overrightarrow {AI}  = {1 \over 2}(\overrightarrow {AB}  + \overrightarrow {AC} )\) (2)

Thay (2) vào (1) ta được:

\(\overrightarrow {AK}  = {1 \over 2}{\rm{[}}\overrightarrow {AB}  + {1 \over 2}(\overrightarrow {AB}  + \overrightarrow {AC} ){\rm{]}}\)

\(\overrightarrow {AK}  = {3 \over 4}\overrightarrow {AB}  + {1 \over 4}\overrightarrow {AC} \)

Bài 1.72 trang 48 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng Oxy cho tam giác đều OAB có cạnh bằng 2, AB song song với Ox, điểm A có hoành độ và tung độ dương.

a) Tìm tọa độ hai đỉnh A và B;

b) Tìm tọa độ trọng tâm G của tam giác OAB.

Gợi ý làm bài

(Xem hình 1.79)

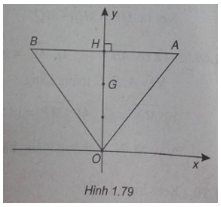
a) Gọi H là trung điểm của AB ta có:

\(OH = {{OA\sqrt 3 } \over 2} = \sqrt 3 ;HA = {{OA} \over 2} = 1\)

Vậy ta có \(A(1;\sqrt 3 )\) và \(B( - 1;\sqrt 3 )\)

b) \(OG = {2 \over 3}OH = {2 \over 3}\sqrt 3 \)

Vậy ta có \(G\left( {0;{{2\sqrt 3 } \over 3}} \right)\)

Giaibaitap.me