Bài 1.52 trang 45 Sách bài tập (SBT) Toán Hình học 10
Cho lục giác đều ABCDEF và M là một điểm tùy ý. Chứng minh rằng:
\(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} = \overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} \)
Gợi ý làm bài
(h.1.65)
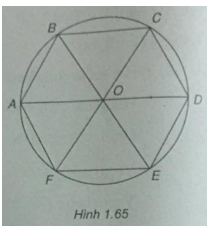
Gọi O là tâm lục giác đều. Khi đó O là trọng tâm của các tam giác đều ACE và BDF.
Do đó, với mọi điểm M ta có:
\(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} = 3\overrightarrow {MO} \)
\(\overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} = 3\overrightarrow {MO} \)
Vậy ta có đẳng thức cần chứng minh.
Bài 1.53 trang 45 Sách bài tập (SBT) Toán Hình học 10
Cho tam giác ABC. Tìm điểm M thỏa mãn điều kiện: \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
Gợi ý làm bài
(h.1.66)
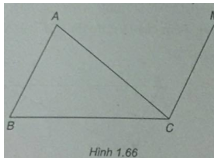
\(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CM} $\)
M là đỉnh của hình bình hành ABCM.
Bài 1.54 trang 45 Sách bài tập (SBT) Toán Hình học 10
Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF = FC. BE cắt trung tuyến AM tại N. Tính \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} \)
Gợi ý làm bài
(h.1.67)
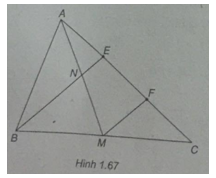
Ta có \(\overrightarrow {AE} = \overrightarrow {FC} \)
Vì MF // BE nên N là trung điểm của AM, suy ra \(\overrightarrow {AN} + \overrightarrow {MN} = \overrightarrow 0 \)
Do đó \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} = \overrightarrow {AF} + \overrightarrow {FC} = \overrightarrow {AC}\)
Giaibaitap.me
Giải bài tập trang 45, 46 bài ôn tập chương I Sách bài tập (SBT) Toán Hình học 10. Câu 1.55: Cho hai điểm A và B. Điểm M thỏa mãn điều kiện...
Giải bài tập trang 46 bài ôn tập chương I Sách bài tập (SBT) Toán Hình học 10. Câu 1.58: Cho hình vuông ABCD, E là trung điểm của CD...
Giải bài tập trang 46 bài đề toán tổng hợp chương I Sách bài tập (SBT) Toán Hình học 10. Câu 1.61: Cho các điểm A'(-4;1), B'(2;4) và C'(2; - 2) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC...
Giải bài tập trang 47 bài đề toán tổng hợp chương I Sách bài tập (SBT) Toán Hình học 10. Câu 1.65: Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA...
