Bài 1.40 trang 44 Sách bài tập (SBT) Toán Hình học 10

a) Cho \(A( - 1;8),B(1;6),C(3;4)\). Chứng minh ba điểm A, B, C thẳng hàng.

b) Cho \(A(1;1),B(3;2),C(m + 4;2m + 1)\). Tìm m để ba điểm A, B, C thẳng hàng.

Gợi ý làm bài

a) \(\overrightarrow {AB}  = (2; - 2),\overrightarrow {AC}  = (4; - 4)\)

Vậy \(\overrightarrow {AC}  = 2\overrightarrow {AB} \) =>ba điểm A, B, C thẳng hàng.

b) \(\overrightarrow {AB}  = (2;1),\overrightarrow {AC}  = (m + 3;2m)\)

Ba điểm A, B, C thẳng hàng \( \Leftrightarrow {{3m} \over 2} = {{2m} \over 2} \Leftrightarrow m = 1\)

Bài 1.41 trang 44 Sách bài tập (SBT) Toán Hình học 10

Cho bốn điểm \(A( - 2; - 3),B(3;7),C(0;3),D( - 4; - 5)\).

Chứng minh rằng hai đường thẳng AB và CD song song với nhau.

Gợi ý làm bài

\(\overrightarrow {AB}  = (5;10),\overrightarrow {CD}  = ( - 4; - 8)\). Ta có: \(\overrightarrow {CD}  =  - {4 \over 5}\overrightarrow {AB} \), vậy hai đường thẳng AB và CD song song hoặc trùng nhau.

Ta có \(\overrightarrow {AC}  = (2;6)\) và \(\overrightarrow {AB} \) không trùng phương vì \({5 \over 2} \ne {{10} \over 6}\)

Vậy AB // CD

Bài 1.42 trang 44 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC. Các điểm \(M(1;1),N(2;3),P(0; - 4)\) lần lượt là trung điểm các cạnh BC, CA, AB. Tính tọa độ các đỉnh của tam giác.

Gợi ý làm bài

(h.1.56)

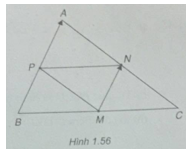
\(\overrightarrow {MN}  = (1;2)\)

\(\overrightarrow {PA}  = ({x_A};{y_A} + 4)\)

Vì \(\overrightarrow {PA}  = \overrightarrow {MN} \) suy ra

\(\left\{ \matrix{
{x_A} = 1 \hfill \cr
{y_A} + 4 = 2 \hfill \cr} \right. = > \left\{ \matrix{
{x_A} = 1 \hfill \cr
{y_A} = - 2 \hfill \cr} \right.\)

Tương tự, ta tính được 

\(\left\{ \matrix{
{x_B} = - 1 \hfill \cr
{y_B} = - 6 \hfill \cr} \right. = > \left\{ \matrix{
{x_C} = 3 \hfill \cr
{y_C} = 8 \hfill \cr} \right.\)

Vậy tọa độ các đỉnh của tam giác là \(A(11; - 2),B( - 1; - 6),C(3;8)\)

Bài 1.43 trang 44 Sách bài tập (SBT) Toán Hình học 10

Cho hình bình hành ABCD. Biết \(A(2; - 3),B(4;5),C(0; - 1)\). Tính tọa độ của đỉnh D.

Gợi ý làm bài

(h.1.57) 

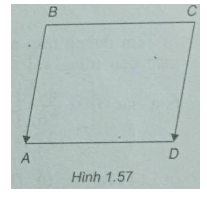
\(\overrightarrow {BA}  = ( - 2; - 8)\)

\(\overrightarrow {CD}  = ({x_D};{y_D} + 1)\). Vì \(\overrightarrow {BA}  = \overrightarrow {CD} \) nên

\(\left\{ \matrix{
{x_D} = - 2 \hfill \cr
{y_D} + 1 = - 8 \hfill \cr} \right. = > \left\{ \matrix{
{x_D} = - 2 \hfill \cr
{y_D} = - 9 \hfill \cr} \right.\)

Vậy tọa độ đỉnh D(-2; -9)
Nhận xét: Ta có thể tính tọa độ đỉnh D dựa vào biểu thức \(\overrightarrow {BD}  = \overrightarrow {BA}  + \overrightarrow {BC} \)

Giaibaitap.me