Bài 1.30 trang 34 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC. Điểm I trên cạnh AC sao cho $$CI = {1 \over 4}CA$$, J là điểm mà 

\(\overrightarrow {BJ}  = {1 \over 2}\overrightarrow {AC}  - {2 \over 3}\overrightarrow {AB} \)

a) Chứng minh \(\overrightarrow {BI}  = {3 \over 4}\overrightarrow {AC}  - \overrightarrow {AB} \)

b) Chứng minh B, I, J thẳng hàng.

c) Hãy dựng điểm J thỏa mãn điều kiện đề bài.

Gợi ý làm bài

(Xem h.1.50)

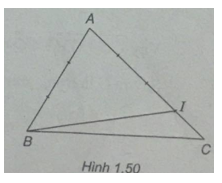
a) \(\overrightarrow {BI}  = \overrightarrow {BA}  + \overrightarrow {AI}  =  - \overrightarrow {AB}  + {3 \over 4}\overrightarrow {AC} \)

b) \({2 \over 3}\overrightarrow {BI}  = {2 \over 3}\left( { - \overrightarrow {AB}  + {3 \over 4}\overrightarrow {AC} } \right) =  - {2 \over 3}\overrightarrow {AB}  + {1 \over 2}\overrightarrow {AC} \)

Vậy \(\overrightarrow {BJ}  = {2 \over 3}\overrightarrow {BI}\)

B, J, I thẳng hàng.

c) Học sinh tự dựng điểm J.

Bài 1.28 trang 34 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho NA = 2NC. Gọi K là trung điểm của MN.

Phân tích vec tơ \(\overrightarrow {AK} \) \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)

Gợi ý làm bài

(h.1.48)

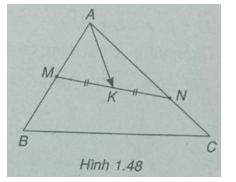
\(\overrightarrow {AK}  = {1 \over 2}(\overrightarrow {AM}  + \overrightarrow {AN} )\)

\( = {1 \over 2}({1 \over 2}\overrightarrow {AB}  + {2 \over 3}\overrightarrow {AC} )\)

\( = {1 \over 4}\overrightarrow {AB}  + {1 \over 3}\overrightarrow {AC} \)

Bài 1.29 trang 34 Sách bài tập (SBT) Toán Hình học 10

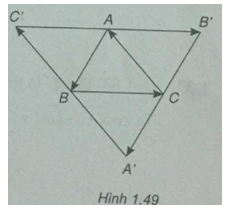
Cho tam giác ABC. Dựng \(\overrightarrow {A'B}  = \overrightarrow {BC} ,\overrightarrow {C'A}  = \overrightarrow {AB} \) và \(\overrightarrow {BC'}  = \overrightarrow {CA} \)

a) Chứng minh rằng A là trung điểm của B'C'

b) Chứng minh các đường thẳng AA', BB', CC' đồng quy

Gợi ý làm bài

a) \(\overrightarrow {BC'}  = \overrightarrow {CA} \) => Tứ giác ACBC' là hình bình hành => \(\overrightarrow {AC'}  = \overrightarrow {CB} \)

\(\overrightarrow {AB'}  + \overrightarrow {AC'}  = \overrightarrow {BC}  + \overrightarrow {CB}  = \overrightarrow {BB}  = \overrightarrow 0 \) =>A là trung điểm của B'C'

b) Vì tứ giác ACBC' là hình bình hành nên CC' chứa trung tuyến của tam giác ABC xuất phát từ đỉnh C. Tương tự như vậy với AA', BB'. Do đó AA', BB', CC' đồng quy tại trọng tâm G của tam giác ABC.

Bài 1.31 trang 34 Sách bài tập (SBT) Toán Hình học 10

Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng với điểm M bất kì ta có \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = 4\overrightarrow {MO} \)

 Gợi ý làm bài

(h.1.51)

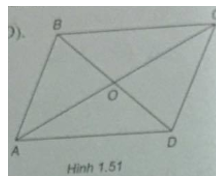
\(\overrightarrow {MA}  + \overrightarrow {MC}  = 2\overrightarrow {MO} \) ( Vì O là trung điểm của AC)

\(\overrightarrow {MB}  + \overrightarrow {MD}  = 2\overrightarrow {MO} \) ( Vì O là trung điểm của BD)

Vậy \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = 4\overrightarrow {MO} \)

Giaibaitap.me