Bài 1.24 trang 33 Sách bài tập (SBT) Toán Hình học 10

Cho hai tam giác ABC và A'B'C'. Chứng minh rằng nếu \(\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'}  = \overrightarrow 0 \) thì hai tam giác đó có cùng trọng tâm.

Gợi ý làm bài

Gọ G và G' lần lượt là trọng tâm của hai tam giác ABC và A'B'C'. Ta có:

\(\overrightarrow {AA'}  = \overrightarrow {AG}  + \overrightarrow {GG'}  + \overrightarrow {G'A'} \)

\(\overrightarrow {BB'}  = \overrightarrow {BG}  + \overrightarrow {GG'}  + \overrightarrow {G'B'} \)

\(\overrightarrow {CC'}  = \overrightarrow {CG}  + \overrightarrow {GG'}  + \overrightarrow {G'C'} \)

Cộng từng vế của ba đẳng thức trên ta được

\(\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'}  = 3\overrightarrow {GG'} \)

Do đó, nếu \(\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'}  = \overrightarrow 0 \) thì \(\overrightarrow {GG'}  = \overrightarrow 0 \) hay G = G'

Chú ý: Từ chứng minh trên cũng suy ra rằng nếu hai tam giác ABC và A'B'C' có cùng trọng tâm thì \(\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'}  = \overrightarrow 0 \) 

Bài 1.25 trang 33 Sách bài tập (SBT) Toán Hình học 10

Cho hai vec tơ không cùng phương \(\overrightarrow a \) và \(\overrightarrow b \). Dựng các vec tơ:

a) \(2\overrightarrow a  + \overrightarrow b \)

b) \(\overrightarrow a  - 2\overrightarrow b \)

c) \( - \overrightarrow a  + {1 \over 2}\overrightarrow b\)

Gợi ý làm bài

(Xem h.1. 45)

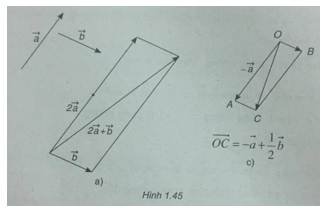
Hãy vẽ trường hợp \(\overrightarrow a  - 2\overrightarrow b \)

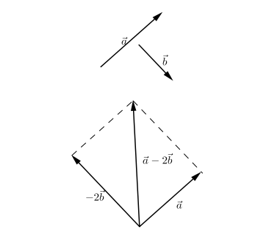
Bài 1.26 trang 33 Sách bài tập (SBT) Toán Hình học 10

Cho lục giác đều ABCDEF tâm O có cạnh a.

a) Phân tích vec tơ \(\overrightarrow {AD} \) theo hai vec tơ  \(\overrightarrow {AB} \) và \(\overrightarrow {AF} \)

b) Tính độ dài của vec tơ \({1 \over 2}\overrightarrow {AB}  + {1 \over 2}\overrightarrow {BC} \) theo a.

Gợi ý làm bài

(Xem h.1.46)

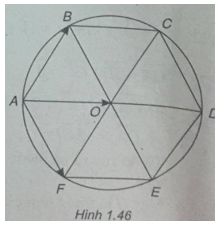
a) \(\overrightarrow {AD}  = 2\overrightarrow {AO}  = 2(\overrightarrow {AB}  + \overrightarrow {AF} ) = 2\overrightarrow {AB}  + 2\overrightarrow {AF} \)

b) \({1 \over 2}\overrightarrow {AB}  + {1 \over 2}\overrightarrow {BC}  = {1 \over 2}(\overrightarrow {AB}  + \overrightarrow {BC} ) = {1 \over 2}\overrightarrow {AC}\)

\( =  > \left| {{1 \over 2}\overrightarrow {AB}  + {1 \over 2}\overrightarrow {BC} } \right| = {1 \over 2}\overrightarrow {AC}  = {1 \over 2}a\sqrt 3  = {{a\sqrt 3 } \over 2}\)

Bài 1.27 trang 33 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC có trung tuyến \(\overrightarrow {AM} \) (M là trung điểm của BC). Phân tích vec tơ \(\overrightarrow {AM} \) theo hai vec tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)

Gợi ý làm bài

(h.1.47)

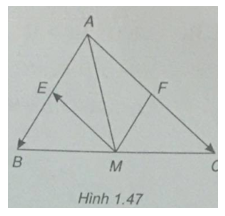
Gọi E, F lần lượt là trung điểm của AB, AC.

Ta có tứ giác AFME là hình bình hành nên \(\overrightarrow {AM}  = \overrightarrow {AE}  + \overrightarrow {AF}  = {1 \over 2}\overrightarrow {AB}  + {1 \over 2}\overrightarrow {AC} \)

Có thể chứng minh cách khác như sau:

Vì M là trung điểm của BC nên \(2\overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {AC} \)

Hay \(\overrightarrow {AM}  = {1 \over 2}(\overrightarrow {AB}  + \overrightarrow {AC} )\)

\( = {1 \over 2}\overrightarrow {AB}  + {1 \over 2}\overrightarrow {AC} \)

Giaibaitap.me