Bài 1.12 trang 23 Sách bài tập (SBT) Toán Hình học 10

Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow 0\)

Gợi ý làm bài

\(\eqalign{
& \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = (\overrightarrow {OA} + \overrightarrow {OC} ) + (\overrightarrow {OB} + \overrightarrow {OD} ) \cr
& = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \cr} \)

Bài 1.13 trang 23 Sách bài tập (SBT) Toán Hình học 10

Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF= FC; BE cắt AM tại N. Chứng minh \(\overrightarrow {NA} \) và \(\overrightarrow {NM} \) là hai vec tơ đối nhau.

Gợi ý làm bài

(h. 1.41)

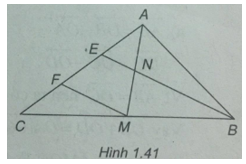
FM // BE vì FM là đường trung bình của tam giác CEB.

Ta có EA = EF . Vậy EN là đường trung bình của tam giác AFM. Vậy $\(\overrightarrow {NA}  =  - \overrightarrow {NM} \)

Bài 1.14 trang 23 Sách bài tập (SBT) Toán Hình học 10

Cho hai điểm phân biệt A và B. Tìm điểm M thỏa mãn một trong các điều kiện sau:

a) \(\overrightarrow {MA}  - \overrightarrow {MB}  = \overrightarrow {BA} \)

b) \(\overrightarrow {MA}  - \overrightarrow {MB}  = \overrightarrow {AB} \)

c) \(\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 \)

Gợi ý làm bài

a) \(\overrightarrow {MA}  - \overrightarrow {MB}  = \overrightarrow {BA}  \Leftrightarrow \overrightarrow {BA}  = \overrightarrow {BA} \). Vậy mọi điểm M đều thỏa mãn hệ thức a).

b) \(\overrightarrow {MA}  - \overrightarrow {MB}  = \overrightarrow {AB}  \Leftrightarrow \overrightarrow {BA}  = \overrightarrow {AB}  \Leftrightarrow A \equiv B\), vô lí. Vậy không có điểm M nào thỏa mãn hệ thức b).

c) \(\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {MA}  =  - \overrightarrow {MB} \). Vậy M là trung điểm của đoạn thẳng AB.

Bài 1.15 trang 23 Sách bài tập (SBT) Toán Hình học 10

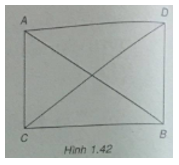
Cho tam giác ABC. Chứng minh rằng nếu \(\left| {\overrightarrow {CA}  - \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA}  - \overrightarrow {CB} } \right|\) thì tam giác ACB là tam giác vuông cân tại C.

Gợi ý làm bài

Vẽ hình bình hành CADB. 

Ta có \(\overrightarrow {CA}  + \overrightarrow {CB}  = \overrightarrow {CD} \), do đó \(\left| {\overrightarrow {CA}  + \overrightarrow {CB} } \right| = CD\)

Vì \(\overrightarrow {CA}  - \overrightarrow {CB}  = \overrightarrow {BA} \), do đó \(\left| {\overrightarrow {CA}  - \overrightarrow {CB} } \right| = BA\)

Từ \(\left| {\overrightarrow {CA}  + \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA}  - \overrightarrow {CB} } \right|\) suy ra CD = AB (h.1.42)

Vậy tứ giác CADB là hình chữ nhật. Ta có tam giác ACB vuông tại C.

Giaibaitap.me