Câu 1 trang 93 SGK Hình học 10
Cho hình chữ nhật \(ABCD\). Biết các đỉnh \(A(5; 1), C(0; 6)\) và phương trình \(CD: x + 2y – 12 = 0\).
Tìm phương trình các đường thẳng chứa các cạnh còn lại.
Trả lời:
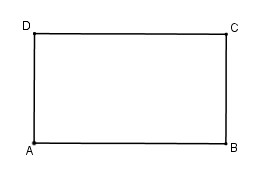
Cạnh \(AB\) là đường thẳng đi qua \(A( 5; 1)\) và song song với \(CD\).
Vì \(CD\) có phương trình \(x + 2y – 12 = 0\) nên phương trình của \(AB\) có dạng:
\(x + 2y + m = 0\)
\(AB\) đi qua \(A(5; 1)\) nên ta có:
\(5 + 2.1 + m = 0 ⇒ m = -7\)
Vậy phương trình của \(AB\) là: \(x + 2y – 7 = 0\)
\(AD\) là đường thẳng qua \(A\) và vuông góc với \(CD\).
Phương trình của \(CD\) là: \(x + 2y – 12 = 0\) nên phương trình của \(AD\) có dạng:
\(2x – y + n = 0\)
\(AD\) đi qua \(A(5, 1)\) cho ta: \(2.5 - 1 + n = 0 ⇒ n = -9\)
Phương trình của \(AD\): \(2x - y - 9 = 0\)
\(CB\) là đường thẳng qua \(C\) và song song với \(AD\) nên phương trình của \(CB\) có dạng:
\(2x – y + p = 0\)
\(CB\) đi qua \(C (0; 6)\) nên: \( 2.0 – 6 + p = 0 ⇒ p = 6\)
Phương trình của \(CB\) là: \(2x – y = 6 = 0\)
Vậy
\(AB: x + y – 7 = 0\)
\(BC : 2x - y + 6 = 0\)
\(AD : 2x – y – 9 = 0\)
Câu 2 trang 93 SGK Hình học 10
Cho \(A(1; 2) B(-3; 1)\) và \(C(4; -2)\). Tìm tập hợp điểm \(M\) sao cho \(M{A^2} + M{B^2} = M{C^2}\)
Trả lời:
Gọi \((x; y)\) là tọa độ của điểm \(M\).
\(\eqalign{
& \overrightarrow {MA} = (x - 1;y - 2) \cr
& \overrightarrow {MB} = (x + 3;y - 1) \cr
& \overrightarrow {MC} = (x - 4;y + 2) \cr} \)
Theo giả thiết, ta có:
\({\left( {x - 1} \right)^2} + {\rm{ }}{\left( {y{\rm{ }} - 2} \right)^2} + {\rm{ }}{\left( {x + {\rm{ }}3} \right)^2} + {\rm{ }}{\left( {y + 1} \right)^2} = {\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}4} \right)^2} + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}2} \right)^2}\)
\(\eqalign{
& \Leftrightarrow {x^2} + {\rm{ }}{y^2} + {\rm{ }}12x{\rm{ }}-{\rm{ }}10y{\rm{ }}-{\rm{ }}5{\rm{ }} = {\rm{ }}0 \cr
& \Leftrightarrow {\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}6} \right)^2} + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}5} \right)^2} = {\rm{ }}66 \cr} \)
Vậy quỹ tích các điểm \(M\) thỏa mãn đẳng thức \(M{A^2} + M{B^2} = M{C^2}\) là đường tròn tâm \(I (-6; 5)\) và bán kính \(R = \sqrt{66}\).
Câu 3 trang 93 SGK Hình học 10
Tìm tập hợp các điểm cách đều hai đường thẳng:
\({\Delta _1} : 5x + 3y – 3 = 0\)
\({\Delta _2}: 5x + 3y + 7 = 0\)
Trả lời:
Gọi \(M(x; y)\) là một điểm bất kì trong mặt phẳng, ta có:
\(\eqalign{
& d(M,{\Delta _1}) = {{|5x + 3y - 3|} \over {\sqrt {{5^2} + {3^2}} }} = {{|5x + 3y - 3|} \over {\sqrt {34} }} \cr
& d(M,{\Delta _2}) = {{|5x + 3y + 7|} \over {\sqrt {{5^2} + {3^2}} }} = {{|5x + 3y + 7|} \over {\sqrt {34} }} \cr} \)
Điểm \(M\) cách đều hai đường thẳng \({\Delta _1},{\Delta _2}\) nên:
\(\eqalign{
& {{|5x + 3y - 3|} \over {\sqrt {34} }} = {{|5x + 3y + 7|} \over {\sqrt {34} }} \cr
& \Leftrightarrow |5x + 3y - 3| = |5x + 3y + 7| \cr} \)
Ta xét hai trường hợp:
(*) \(5x + 3y – 3 = - (5x + 3y + 7) ⇔ 5x + 3y + 2 = 0\)
(**) \(5x + 3y – 3 = 5x + 3y + 7\) (vô nghiệm)
Vậy tập hợp các điểm \(M\) cách đều hai đường thẳng \({\Delta _1},{\Delta _2}\) là đường thẳng \(Δ: 5x + 3y + 2 = 0\)
Dễ thấy \(Δ\) song song với \({\Delta _1},{\Delta _2}\) và hai đường thẳng \({\Delta _1},{\Delta _2}\) nằm về hai phía đối với \(Δ\).
Câu 4 trang 93 SGK Hình học 10
Cho đường thẳng \(Δ: x – y + 2\) và hai điểm \(O(0; 0); A(2; 0)\)
a) Tìm điểm đối xứng của \(O\) qua \(Δ\)
b) Tìm điểm \(M\) trên \(Δ\) sao cho độ dài đường gấp khúc \(OMA\) ngắn nhất.
Trả lời:
a) Gọi \(H\) là hình chiếu của \(O\) trên \(Δ, H\) là giao điểm của đường thẳng qua \(O\) và vuông góc với \(Δ\).
\(\overline {OH} = (x;y)\)
\( Δ: x – y + 2 = 0\) có vecto chỉ phương \(\overrightarrow u (1;1)\)
\(\overrightarrow {OH} \bot \Delta \Rightarrow 1.x + 1.y = 0 \Leftrightarrow x + y = 0\)
Tọa độ điểm \(H\) là nghiệm của hệ phương trình:
\(\left\{ \matrix{
x + y = 0 \hfill \cr
x - y + 2 = 0 \hfill \cr} \right. \Rightarrow H( - 1;1)\)
Gọi \(O’\) là đỉnh đối xứng của \(O\) qua \(Δ\) thì \(H\) là trung điểm của đoạn thẳng \(OO’\)
\(\eqalign{
& {x_H} = {{{x_O} + {x_{O'}}} \over 2} \Leftarrow - 1 = {{0 + {x_{O'}}} \over 2} \Rightarrow {x_{O'}} = - 2 \cr
& {y_H} = {{{y_O} + {y_{O'}}} \over 2} \Leftarrow - 1 = {{0 + {y_{O'}}} \over 2} \Rightarrow {y_{O'}} = 2 \cr} \)
Vậy \(O’(-2;2)\).
b) Nối \(O’A\) cắt \(Δ\) tại \(M\)
Ta có: \(OM = O’M\)
\(⇒ OM + MA = O’M + MA = O’A\)
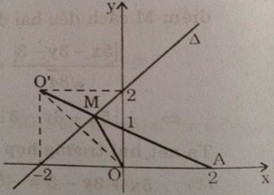
Giả sử trên \(Δ\) có một điểm \(M’ ≠ M\), ta có ngay:
\(OM’ +M’A > O’A\)
Vậy điểm \(M\), giao điểm của \(O’A\) với \(Δ\), chính là điểm thuộc \(Δ\) mà độ dài của đường gấp khúc \(OMA\) ngắn nhất.
\(A(2; 0); O(-2; 2)\) nên \(O’A\) có hệ phương trình: \(x + 2y – 2 = 0\)
Tọa độ của điểm \(M\) là nghiệm của hệ:
\(\left\{ \matrix{
x + 2y - 2 = 0 \hfill \cr
x - y + 2 = 0 \hfill \cr} \right. \Rightarrow M( - {2 \over 3},{4 \over 3})\)
Giaibaitap.me
Giải bài tập trang 93 bài ôn tập chương III - Phương pháp tọa độ trong mặt phẳng Sách giáo khoa (SGK) Hình học 10. Câu 5: Tìm tọa độ điểm ...
Giải bài tập trang 94 bài ôn tập chương III - Phương pháp tọa độ trong mặt phẳng Sách giáo khoa (SGK) Hình học 10. Câu 1: Phương trình nào sau đây là phương trình đường cao của tam giác vẽ từ...
Giải bài tập trang 94, 95 bài ôn tập chương III - Phương pháp tọa độ trong mặt phẳng Sách giáo khoa (SGK) Hình học 10. Câu 5: Tìm mệnh đề sai trong các mệnh đề sau...
Giải bài tập trang 95 bài ôn tập chương III - Phương pháp tọa độ trong mặt phẳng Sách giáo khoa (SGK) Hình học 10. Câu 7: Cho hai đường thẳng...
