Câu 5 trang 93 SGK Hình học 10

Cho ba điểm \(A(4; 3), B(2; 7), C(-3; -8)\)

a) Tìm tọa độ điểm \(G\) , trực tâm \(H\) của tam giác \(ABC\).

b) Tìm \(T\) là trực tâm của đường tròn ngoại tiếp tam giác \(ABC\). Chứng minh \(T, G, H\) thẳng hàng.

c) Viết phương trình đường tròn ngoại tiếp tam giác \(ABC\).

Trả lời:

Ta có:

\(\eqalign{
& {x_G} = {{{x_A} + {x_B} + {x_C}} \over 3} \Rightarrow {x_G} = {{4 + 2 - 3} \over 3} = 1 \cr
& {y_G} = {{{y_A} + {y_B} + {y_C}} \over 3} \Rightarrow {y_G} = {{3 + 7 - 8} \over 3} = {2 \over 3} \cr} \)

Vậy \(G\left(1,{2 \over 3}\right)\)

Gọi \((x; y)\) là tọa độ của \(H\)

\(\eqalign{
& \overrightarrow {AH} = (x - 4,y - 3);\overrightarrow {BC} = ( - 5, - 15) \cr
& \overrightarrow {BH} = (x - 2,y - 7);\overrightarrow {AC} = ( - 7, - 11) \cr
& \overrightarrow {AH} \bot \overrightarrow {BC} \Leftrightarrow \overrightarrow {AH} .\overrightarrow {BC} = 0 \cr
& \Leftrightarrow - 5(x - 4) - 15(y - 3) = 0 \Leftrightarrow x + y - 13 = 0 \cr
& \overrightarrow {BH} \bot \overrightarrow {AC} \Leftrightarrow \overrightarrow {BH} .\overrightarrow {AC} = 0 \cr
& \Leftrightarrow - 7(x - 2) - 11(y - 7) = 0 \Leftrightarrow 7x + 11y - 91 = 0 \cr} \)

Tọa độ điểm H là nghiệm của hệ phương trình:

\(\left\{ \matrix{
x + y - 13 = 0 \hfill \cr
7x + 11y - 91 = 0 \hfill \cr} \right. \Rightarrow H(13;0)\)

b) Tâm \(T\) của đường tròn ngoại tiếp tam giác \(ABC\) thỏa mãn điều kiện

\(TA = TB = TC ⇒ TA^2= TB^2= TC^2\), cho ta:

\({\left( {x{\rm{ }}-{\rm{ }}4} \right)^2} +{\left( {y-3} \right)^2} = {\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}2} \right)^2} + {\left( {y{\rm{ }}-{\rm{ }}7} \right)^2} \Leftrightarrow {\rm{ }}x{\rm{ }}-{\rm{ }}2y{\rm{ }} + {\rm{ }}7 =0\)

\({\left( {x{\rm{ }}-{\rm{ }}4} \right)^2} +{\left( {y-3} \right)^2} = {\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}3} \right)^2} + {\rm{ }}{\left( {y +8} \right)^2} \Leftrightarrow {\rm{ }}7x{\rm{ }} + 11y +24 = 0\)

Do đó tọa độ tâm \(T\) của đường tròn ngoại tiếp tam giác \(ABC) là nghiệm của hệ:

\(\left\{ \matrix{
x - 2y + 7 = 0 \hfill \cr
7x + 11y + 24 = 0 \hfill \cr} \right. \Rightarrow T( - 5;1)\)

Ta có: \(\overrightarrow {TH}  = ( - 18;1);\overrightarrow {TG}  = (6;{-1 \over 3})\)

Ta có: \(\overrightarrow {TH}  = {3}\overrightarrow {TG} \)

Vậy ba điểm \(H, G, T\) thẳng hàng.

c) Đường tròn ngoại tiếp tam giác \(ABC\) có tâm \(T(-5; 1)\), bán kính \(R = AT = \sqrt{85}\)

\({R^2} = A{T^2} = {\left( { - 5-{\rm{ }}4} \right)^2} + {\rm{ }}{\left( {1-3} \right)^2} = 85\)

Vậy phương trình đường tròn ngoại tiếp tam giác \(ABC\) là:

\((x + 5)^2+ (y – 1)^2= 85\)

Câu 6 trang 93 SGK Hình học 10

Lập phương trình hai đường phân giác của các góc tạo bởi đường thẳng \(3x – 4y + 12 = 0\) và \(12x+5y-7 = 0\)

Trả lời:

Gọi \(M(x; y)\) thuộc đường phân giác của góc tạo bởi đường thẳng trên.

Khi đó, khoảng cách từ \(M\) đến \(d_1 : 3x  - 4y + 12 = 0\) là:

 \(d(M,{d_1}) = {{|3x - 4y + 12|} \over {\sqrt {9 + 16} }} = {{|3x - 4y + 12|} \over 5}\)

Khoảng cách từ \(M\) đến \(d_2: 12x + 15y – 7 = 0\) là:

\(d(M,{d_2}) = {{|12x + 5y - 7|} \over {\sqrt {144 + 25} }} = {{|12x + 5y - 7|} \over {13}}\)

Ta có: \(M\) thuộc đường  phân giác của góc tạo bởi hai đường thẳng \(d_1\) và \(d_2\) nên cách đều hai đường thẳng đó.Suy ra: 

\(\eqalign{
& d(M,{d_1}) = d(M,{d_2}) \Leftrightarrow {{|3x - 4y + 12|} \over 5} = {{|12x + 5y - 7|} \over {13}} \cr
& \Leftrightarrow \left[ \matrix{
{{3x - 4y + 12} \over 5} = {{12x + 5y - 7} \over {12}} \hfill \cr
{{3x - 4y + 12} \over 5} = - {{12x + 5y - 7} \over {13}} \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
21x + 77y - 191 = 0 \hfill \cr
99x - 27y + 121 = 0 \hfill \cr} \right. \cr} \)

Vậy ta có phương trình của hai đường phân giác của các góc tạo bởi \(d_1\) và \(d_2\) là:

\(\Delta _1: 21x + 77y – 191 = 0\)

\(\Delta _2: 99x – 27y + 121 = 0\)

Câu 7 trang 93 SGK Hình học 10

Cho đường tròn \((C)\) có tâm \(I(1, 2)\) và bán kính bằng \(3\). Chứng minh rằng tập hợp các điểm \(M\) từ đó ta sẽ được hai tiếp tuyến với \((C)\) tạo với nhau một góc \(60^0\) là một đường tròn. Hãy viết phương trình đường tròn đó.

Trả lời:

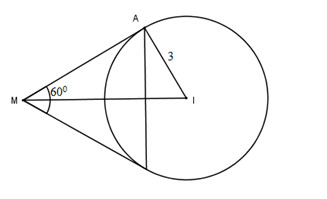
Theo tính chất của tiếp tuyến ta có: \(\widehat {AMI} = {30^0}\)

\(IM = {{IA} \over {\sin \widehat {AMI}}} = {3 \over {\sin {{30}^0}}} = {3 \over {{1 \over 2}}} = 6\)

Gọi tọa độ của \(M\) là \((x ;y)\) Ta có:

\(O{M^2} = {(x - 1)^2} + {(y - 2)^2} = 36\)

Vậy quỹ tích \(M\) là đường tròn tâm \(I (1; 2)\), bán kính \(R = 6\)

Phương trình đường tròn là: \({(x - 1)^2} + {(y - 2)^2} = 36\)

Câu 8 trang 93 SGK Hình học 10

Tìm góc giữa hai đường thẳng \(\Delta_1\) và \(\Delta_2\) trong các trường hợp sau:

a) \(\Delta_1\): \(2x + y – 4 = 0\) ; \(\Delta_2\): \(5x – 2y + 3 = 0\)

b) \(\Delta_1\): \(y = -2x + 4\)  ;   \({\Delta _2}:y = {1 \over 2}x + {3 \over 2}\)        

Trả lời:

a) Vecto pháp tuyến \(\Delta_1\) là \(\overrightarrow {{n_1}}  = (2;1)\)

Vecto pháp tuyến \({\Delta _2}\) là \(\overrightarrow {{n_2}}  = (5; - 2)\)

\(\eqalign{
& \cos ({\Delta _1},{\Delta _2}) = {{|\overrightarrow {{n_1}} .\overrightarrow {{n_2}} |} \over {|\overrightarrow {{n_1}} |.|\overrightarrow {{n_2}} |}} = {{|2.5 + 1.( - 2)|} \over {\sqrt 5 .\sqrt 9 }} = {8 \over {\sqrt {145} }} \cr
& \Rightarrow ({\Delta _1},{\Delta _2}) \approx {48^0}21'59'' \cr} \)

b) \(y  = -2x + 4 ⇔ 2x + y – 4 = 0\)

 \(y = {1 \over 2}x + {3 \over 2} \Leftrightarrow x - 2y + 3 = 0\)

Vì \(2.1 + 1.(-2) = 0 ⇔\Delta_1⊥{\Delta _2}\)

Chú ý:

_  Hệ số góc của  \(\Delta_1\) là \(k = -2\)

_ Hệ số góc của \({\Delta _2}\) là \(k' = {1 \over 2}\)

Vì \(k.k' = 2.{1 \over 2} =  - 1 \Rightarrow {\Delta _1} \bot {\Delta _2}\)

Câu 9 trang 93 SGK Hình học 10

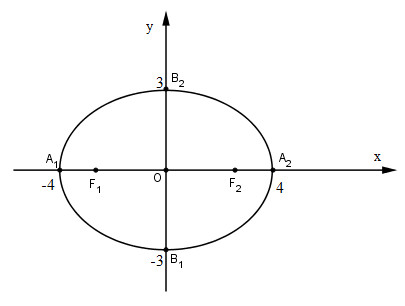
Cho elip \((E) = {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) . Tìm tọa độ các đỉnh, các tiêu điểm và vẽ elip đó.

Trả lời:

Phương trình chính tắc của Elip \((E) = {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) có dạng là:

\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)

Ta có:

\(\eqalign{
& \left\{ \matrix{
{a^2} = 16 \hfill \cr 
{b^2} = 9 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 4 \hfill \cr 
b = 3 \hfill \cr} \right. \cr 
& c = \sqrt {{a^2} - {b^2}} = \sqrt 7 \cr} \)

_ Tọa độ các đỉnh \(A_1(-4;0), A_2(4; 0), B_1(0; -3)\) và \(B_2(0; 3)\)

_ Tọa độ các tiêu điểm \(F_1(-\sqrt7; 0)\) và \(F_2(\sqrt7; 0)\)

Giaibaitap.me