Bài 1 trang 44 SGK Đại số 10 nâng cao

Tìm tập xác định của mỗi hàm số sau

\(\eqalign{
& a)\,y = {{3x + 5} \over {{x^2} - x + 1}} \cr
& b)\,y = {{x - 2} \over {{x^2} - 3x + 2}} \cr
& c)\,y = {{\sqrt {x - 1} } \over {x - 2}} \cr
& d)\,y = {{{x^2} - 2} \over {(x + 2)\sqrt {x + 1} }} \cr} \)

Giải

a)

Vì x² – x + 1 ≠ 0 với mọi \(x ∈\mathbb R\) nên tập xác định của hàm số là \(D =\mathbb R\)

b)

Hàm số xác định 

\( \Leftrightarrow \,{x^2} - 3x + 2 \ne 0 \Leftrightarrow \left\{ \matrix{
x \ne 1 \hfill \cr
x \ne 2 \hfill \cr} \right.\)

Vậy \(D{\rm{ }} = {\rm{ }}\mathbb R\backslash \left\{ {1,{\rm{ }}2} \right\}\)

c)

Hàm số xác định 

\( \Leftrightarrow \left\{ \matrix{
x - 1 \ge 0 \hfill \cr
x - 2 \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ge 1 \hfill \cr
x \ne 2 \hfill \cr} \right.\)

Vậy \(D = [1; 2) ∪ (2; +∞)\)

d)

Hàm số xác định 

\( \Leftrightarrow \left\{ \matrix{
x + 2 \ne 0 \hfill \cr
x + 1 > 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ne- 2 \hfill \cr
x > - 1 \hfill \cr} \right. \Leftrightarrow x > - 1\)

Vậy \(D= (-1; +∞)\)

Bài 2 trang 44 SGK Đại số 10 nâng cao

Biểu đồ hình 2.8 cho biết số triệu tấn gạo xuất khẩu của Việt Nam trong các năm từ 2000 đến 2005. Biểu đồ này cho ta một hàm số. Hãy cho biết tập xác định và nêu một vài giá trị của hàm số đó.

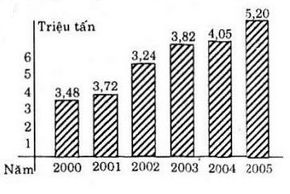
Giải

Tập xác định D = {2000,..., 2005}. Kí hiệu hàm số là f(x).

Ta có:

f(2000) = 3,84; f(2001) = 3,72; ....; f(2005) = 5,2

Bài 3 trang 45 SGK Đại số 10 nâng cao

Hình 2.9 là đồ thị của một hàm số có tập xác định là \(\mathbb R\).

Dựa vào đồ thị, hãy lập bảng biến thiên của hàm số đó.

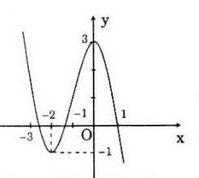
Giải

Bảng biến thiên của hàm số:

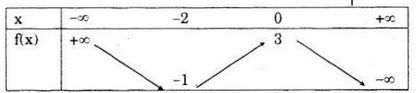
Bài 4 trang 45 SGK Đại số 10 nâng cao

Khảo sát sự biến thiên của mỗi hàm số sau và lập bảng biến thiên của nó:

a) y = x² + 2x – 2 trên mỗi khoảng \((-∞; -1)\) và \((-1, +∞)\)

b) y = -2x + 4x + 1  trên mỗi khoảng \((-∞; 1)\) và \((1, +∞)\)

c) \(y = {2 \over {x - 3}}\) trên mỗi khoảng \((-∞; 3)\) và \((3, +∞)\)

Giải

a)

+ Với mọi x₁; x₂ ∈  \((-∞; -1)\) và x₁ ≠ x₂ ta có:

f(x₂) – f(x₁) = x₂² + 2x₂ – 2 – (x₁² + 2x₁ – 2)

 = x₂² – x₁² + 2(x₂ – x₁) = (x₂ – x₁)(x₁ + x₂ + 2)

\(\Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {x_1} + {x_2} + 2\)

Vì x₁ < -1 và x₂ < -1 nên x₁ + x₂ + 2 < 0

Nên \( \Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} < 0\)

Vậy hàm số y = x² + 2x – 2 nghịch biến trên \((-∞; -1)\)

+ Với mọi x₁; x₂ ∈ \((-1, +∞)\) và x₁ ≠ x₂ ta có:

\({{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {x_1} + {x_2} + 2 > 0\)

( Vì x₁ > -1; x₂ > -1)

Vậy hàm số y =  x² + 2x – 2 đồng biến trên \((-1, +∞)\)

b)

+ Với mọi x₁; x₂ ∈ \((-∞; 1)\) và x₁ ≠ x₂ ta có:

f(x₂) – f(x₁) = (-2x₂² + 4x₂ + 1) – (-2x₁² + 4x₁ + 1)

= -2(x₂² - x₁²) + 4(x₂ - x₁) = 2(x₂ - x₁)(2 – x₁ – x₂)

\( \Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = 2(2 - {x_1} - {x_2})\)

Vì x₁ < 1 và x₂ < 1 nên 2 - x₁ – x₂ > 0

Vậy hàm số y = -2x + 4x + 1 đồng biến trên khoảng \((-∞; 1)\)

+ Với mọi x₁; x₂ ∈ \((1; +∞)\) và x₁ ≠ x₂ ta có:

\({{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = 2(2 - {x_1} - {x_2}) < 0\)

(vì x₁ > 1 và x₂ > 1 )

Vậy hàm số số y = -2x + 4x + 1 nghịch biến trên khoảng \((1; +∞)\)

c)

+ Với x₁, x₂ ∈ \((- ∞; 3)\) với x₁ ≠ x₂ ta có:

 \(\eqalign{
& f({x_2}) - f({x_1}) = {2 \over {{x_2} - 3}} - {2 \over {{x_1} - 3}} \cr 
& = {{2({x_1} - 3) - 2({x_2} - 3)} \over {({x_1} - 3)({x_2} - 3)}} = {{2({x_1} - {x_2})} \over {({x_1} - 3)({x_2} - 3)}} \cr 
& \Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {{ - 2} \over {({x_1} - 3)({x_2} - 3)}} \cr} \)

(vì x₁ < 3; x₂ < 3 nên (x₁ – 3)(x₂ – 3) > 0)

\(\Rightarrow {{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}}<0\)

Vậy hàm số \(y = {2 \over {x - 3}}\)  nghịch biến trên \((- ∞; 3)\)

+ Với x₁, x₂ ∈ \((3; +∞)\) với x₁ ≠ x₂ ta có:

\({{f({x_2}) - f({x_1})} \over {{x_2} - {x_1}}} = {{ - 2} \over {({x_1} - 3)({x_2} - 3)}} < 0\)

(vì x₁ > 3; x₂ > 3 nên (x₁ – 3)(x₂ – 3) > 0)

Vậy hàm số \(y = {2 \over {x - 3}}\) nghịch biến trên \((3; + ∞)\) 

Giaibaitap.me