Câu 64 trang 167 Sách bài tập (SBT) Toán 9 Tập 1
Cho hình 76, trong đó hai đường tròn (O) và (O’) tiếp xúc nhau tại A. Chứng minh rằng các tiếp tuyến Bx và Cy song song với nhau.
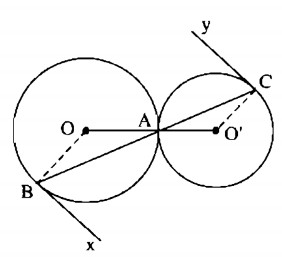
Giải:
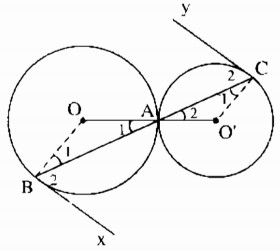
Ta có: O, A, O’ thẳng hàng
C, A, B thẳng hàng
Suy ra: \(\widehat {OAB} = \widehat {OBA}\) (đối đỉnh) (1)
Tam giác AOB cân tại O
Suy ra: \(\widehat {OAB} = \widehat {OBA}\) (2)
Tam giác AO’C cân tại O’
Suy ra: \(\widehat {O'AC} = \widehat {O'CA}\) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {OBA} = \widehat {O'CA}\)
Suy ra OB // O’C (vì có cặp góc so le trong bằng nhau)
Lại có: Bx ⊥ OB (tính chất tiếp tuyến)
Suy ra: Bx ⊥O’C
Mà: Cy ⊥ O’C ( tính chất tiếp tuyến)
Suy ra: Bx // Cy.
Câu 65 trang 167 Sách bài tập (SBT) Toán 9 Tập 1
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B như trên hình 77.
Biết OA = 15cm, O’A = 13cm, AB = 24cm.
Tính độ dài OO’.
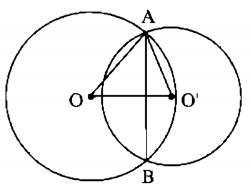
Giải:
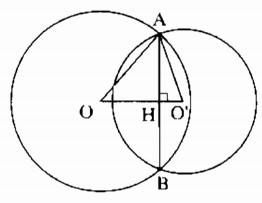
Gọi H là giao điểm của AB và OO’.
Vì OO’ là đường trung trực của AB nên:
OO’ ⊥ AB tại H.
Suy ra: \(HA = HB = {1 \over 2}AB = {1 \over 2}.24 = 12\) (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông
AOH, ta có: AO2 = OH2 + AH2
Suy ra: OH2 = OA2 - AH2 = 152 – 122 = 81
OH = 9 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AO’H, ta có:
AO’2 = O’H2 + AH2
Suy ra: O’H2 = O’A2 – AH2 = 132 – 122 = 25
O’H = 5 (cm)
Vậy OO’ = OH + O’H = 9 + 5 = 14 (cm).
Câu 66 trang 167 Sách bài tập (SBT) Toán 9 Tập 1
Cho hai đường tròn (O), (O’) tiếp xúc nhau tại A như trên hình 78. Chứng minh rằng các bán kính OB và O’C song song với nhau.
Giải:
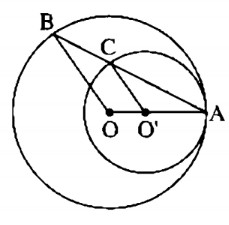
Ta có: OA = OB (= R)
Suy ra tam giác AOB cân tại O
Hay \(\widehat {OAB} = \widehat {OBA}\) (1)
Ta có: O’A = O’C ( = R’ )
Suy ra tam giác AO’C cân tại O’
Hay \(\widehat {O'AC} = \widehat {O'CA}\) (2)
Từ (1) và (2) suy ra: \(\widehat {OBA} = \widehat {O'CA}\)
Suy ra: OB // O’C ( vì có hai góc ở vị trí đồng vị bằng nhau).
Câu 67 trang 167 Sách bài tập (SBT) Toán 9 Tập 1
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ các đường kính AOC, AO’D. Chứng minh rằng ba điểm C, B, D thẳng hàng và AB ⊥ CD.
Giải:
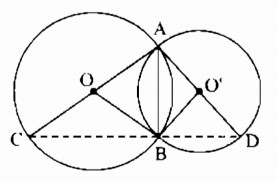
Tam giác ABC nội tiếp trong đường tròn
(O) có AC là đường kính nên \(\widehat {ABC} = 90^\circ \)
Ta có:
\(\widehat {CBD} = \widehat {ABC} + \widehat {ABD} = 90^\circ + 90^\circ = 180^\circ \)
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD.
Giaibaitap.me
Giải bài tập trang 164, 165 bài 6 Tính chất của hai tiếp tuyến cắt nhau Sách bài tập (SBT) Toán 9 tập 2. Câu 51: Cho nửa đường tròn tâm O đường kính AB...
Giải bài tập trang 165 bài 6 Tính chất của hai tiếp tuyến cắt nhau Sách bài tập (SBT) Toán 9 tập 2. Câu 52: Cho đường tròn (I) nội tiếp tam giác ABC...
Giải bài tập trang 165, 166 bài 6 Tính chất của hai tiếp tuyến cắt nhau Sách bài tập (SBT) Toán 9 tập 2. Câu 57: Chứng minh rằng nếu tam giác ABC có chu vi 2p,bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức...
Giải bài tập trang 165 bài 6 Tính chất của hai tiếp tuyến cắt nhau Sách bài tập (SBT) Toán 9 tập 2. Câu 56: Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A ; AH)...
