Câu 4 trang 60 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho hàm số \(y = f\left( x \right) = {2 \over 3}x + 5\) với $x \in R$
Chứng minh rằng hàm số đồng biến trên R.
Gợi ý làm bài:
Xét hàm số \(y = f\left( x \right) = {2 \over 3}x + 5\)
Với hai số \(x_1\) và \(x_2\) thuộc R, ta có:
\({{\rm{y}}_1} = f\left( {{x_1}} \right) = {2 \over 3}{x_1} + 5\)
\({{\rm{y}}_2} = f\left( {{x_2}} \right) = {2 \over 3}{x_2} + 5\)
Nếu \({x_1} < {x_2}\) thì \({x_2} - {x_1} > 0\)
Khi đó:
\(f\left( {{x_2}} \right) - f\left( {{x_1}} \right)\)
\(= \left( {{2 \over 3}{x_2} + 5} \right) - \left( {{2 \over 3}{x_1} + 5} \right) = {2 \over 3}\left( {{x_2} - {x_1}} \right) > 0\)
Suy ra: \(f\left( {{x_2}} \right) > f\left( {{x_1}} \right)\)
Vậy hàm số đồng biến trên R.
Câu 5 trang 61 Sách Bài Tập (SBT) Toán 9 Tập 1
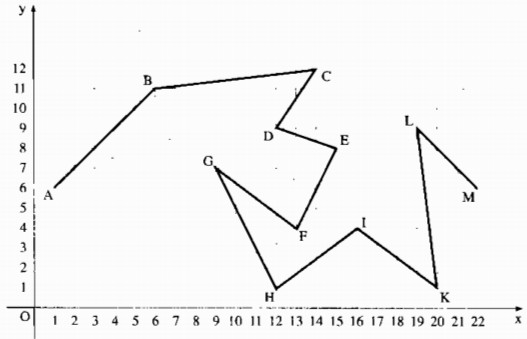
Biểu diễn các điểm sau đây trên cùng một hệ trục tọa độ. Nối theo thứ tự các điểm đã cho bằng các đoạn thẳng để được một đường gấp khúc với điểm đầu là điểm A, điểm cuối là M.
|
A(1; 6) |
B(6; 11) |
C(14; 12) |
D(12; 9) |
|
E(15; 8) |
F(13; 4) |
G(9; 7) |
H(12; 1) |
|
I(16; 4) |
K(20; 1) |
L(19; 9) |
M(22; 6) |
Gợi ý làm bài:
Dựng hệ trục tọa độ Oxy, rồi dựng các điểm theo tọa độ của chúng, nối theo thứ tự các điểm , ta được một đường gấp khúc như hình dưới:
Giaibaitap.me
Giải bài tập trang 61, 62 bài 2 hàm số bậc nhất Sách bài tập (SBT) Toán 9 tập 1. Câu 6: Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b xét xem hàm số nào nghịch biến...
Giải bài tập trang 61, 62, 63 bài 2 hàm số bậc nhất Sách bài tập (SBT) Toán 9 tập 1. Câu 10: Chứng minh rằng hàm số bậc nhất y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0....
Giải bài tập trang 64 bài 3 Đồ thị của hàm số y=ax+b (a≠0) Sách bài tập (SBT) Toán 9 tập 1. Câu 14: Vẽ đồ thị của các hàm số sau trên cũng một mặt phẳng tọa độ...
Giải bài tập trang 65, 66 bài 4 đường thẳng song song và đường thẳng cắt nhau Sách bài tập (SBT) Toán 9 tập 1. Câu 18: Hãy xác định hệ số a trong mỗi trường hợp sau...
