A. Trắc nghiệm

Bài 3.39 trang 74 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Trong các khẳng định sau, khẳng định nào đúng?

A. Không có tứ giác nào mà không có góc tù.

B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.

C. Nếu tứ giác có hai góc tù thì góc còn lại phải nhọn.

D. Không có tứ giác nào có ba góc tù.

Phương pháp:

Sử dụng định lí tổng các góc trong một tứ giác bằng \(360^0\) và lấy các ví dụ cụ thể trong từng trường hợp để tìm ra khẳng định đúng.

Lời giải:

* Khẳng định A sai vì có xảy ra trường hợp tứ giác mà không có góc tù.

Chẳng hạn như hình chữ nhật có bốn góc vuông, tức là hình chữ nhật không có góc tù.

* Khẳng định B.

Tứ giác có ba góc nhọn thì tổng số đo của ba góc bé hơn: 90^o . 3 = 270^o.

Khi đó, góc còn lại sẽ lớn hơn: 360^o – 270^o = 90^o.

Do đó, góc còn lại là góc tù nên khẳng định B đúng.

* Khẳng định C sai vì có thể xảy ra trường hợp tứ giác có hai góc tù, một góc vuông và một góc nhọn.

Ví dụ: Tứ giác ABCD có \(\widehat A = {100^o};\widehat B = {100^o};\widehat C = {90^o};\widehat D = {70^o}\)

* Khẳng định D sai vì có thể xảy ra trường hợp tứ giác có ba góc tù.

Ví dụ: Tứ giác MNPQ có \(\widehat M = {100^o};\widehat N = {110^o};\widehat P = {120^o};\widehat Q = {30^o}\).

Vậy khẳng định B là đúng.

Bài 3.40 trang 74 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?

a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.

b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.

c) Tứ giác có ba góc vuông là hình chữ nhật.

d) Tứ giác có ba cạnh bằng nhau là hình thoi.

Phương pháp:

Sử dụng định nghĩa của hình bình hành, hình chữ nhật, hình thoi để tìm ra các khẳng định đúng, khằng định sai.

Lời giải: 

• Khẳng định a) sai vì tứ giác có hai đường chéo bằng nhau thì chưa chắc tứ giác đó là hình bình hành.

• Khẳng định b) sai vì tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành, còn tứ giác có hai cặp cạnh bằng nhau thì chưa khẳng định được là hình bình hành.

• Khẳng định c) đúng.

Tứ giác có ba góc vuông thì số đo của góc còn lại là:

360^o – 90^o . 3 = 90^o.

Khi đó, số đo của góc còn lại cũng là góc vuông.

Do đó, tứ giác đã cho có bốn góc vuông nên tứ giác đó là hình chữ nhật.

• Khẳng định d) sai vì tứ giác có bốn cạnh bằng nhau mới là hình thoi.

Vậy khẳng định c) đúng; các khẳng định a), b), d) sai.

Bài 3.41 trang 74 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?

a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.

b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.

c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.

d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành.

Phương pháp:

Sử dụng các dấu hiệu nhận biết của các hình đã học

Lời giải: 

a) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.

Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật. 

Nên tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.

Do đó khẳng định a) đúng.

b) Tứ giác có hai cặp cạnh đối diện bằng nhau là hình bình hành.

Nên tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.

Do đó khẳng định b) là đúng.

c) Tứ giác có hai cạnh song song là hình thang.

Hình thang có và hai đường chéo bằng nhau là hình thang cân.

Nên tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.

Do đó khẳng định c) đúng.

d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau nhưng không song song thì không là hình bình hành.

Do đó khẳng định d) sai.

Vậy các khẳng định a), b), c) đúng; khẳng định d) sai.

B. Tự luận

Bài 3.42 trang 74 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân

Phương pháp:

Giả sử tứ giác ABCD có hai đường chéo bằng nhau AC = BD và AD  = BC. Chứng minh ABCD là hình thang mà AC = BD nên ABCD là hình thang cân.

Lời giải: 

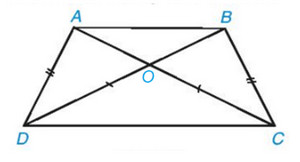
Gọi O là giao điểm của AC và BD.

Xét ∆ABC và ∆BAD có:

AD = BC (giả thiết)

AC = BD (giả thiết)

Cạnh AB chung

Do đó ∆ABC = ∆BAD (c.c.c)

Suy ra \(\widehat {A{\rm{D}}B} = \widehat {ACB}\) (hai góc tương ứng).

Xét ∆ACD và ∆BDC có:

AD = BC (giả thiết)

AC = BD (giả thiết)

Cạnh CD chung

Do đó ∆ADC = ∆BCD (c.c.c)

Suy ra \(\widehat {DAC} = \widehat {CB{\rm{D}}}\) (hai góc tương ứng).

Xét ∆OAD và ∆OBC có:

\(\widehat {A{\rm{D}}B} = \widehat {ACB}\) (chứng minh trên)

AD = BC (giả thiết)

\(\widehat {DAC} = \widehat {CB{\rm{D}}}\) (chứng minh trên)

Do đó ∆OAD = ∆OBC (g.c.g).

Suy ra OA = OB; OC = OD (các cặp cạnh tương ứng).

Khi đó, các tam giác OAB, OCD là tam giác cân tại O.

Suy ra \(\widehat {OAB} = \widehat {OBA};\widehat {OC{\rm{D}}} = \widehat {O{\rm{D}}C}\)

Xét ∆OAB và ∆OCD cân tại O có:

• \(\widehat {AOB} = \widehat {CO{\rm{D}}}\) (hai góc đối đỉnh)

• \(\widehat {OAB} = \widehat {OBA};\widehat {OC{\rm{D}}} = \widehat {O{\rm{D}}C}\)

• \(\widehat {OAB} + \widehat {OBA} + \widehat {AOB} = \widehat {OC{\rm{D}}} + \widehat {O{\rm{D}}C} + \widehat {CO{\rm{D}}} = {180^o}\)

\(\begin{array}{l}\widehat {OAB} + \widehat {OBA} = \widehat {OC{\rm{D}}} + \widehat {O{\rm{D}}C}\\2\widehat {OAB} = 2\widehat {OC{\rm{D}}}\end{array}\)

Suy ra \(\widehat {OAB} = \widehat {OC{\rm{D}}}\) mà hai góc này ở vị trí so le trong.

Do đó AB // CD.

Tứ giác ABCD có AB // CD nên ABCD là hình thang.

Hình thang ABCD có hai đường chéo AC = BD.

Do đó tứ giác ABCD là hình thang cân.

Vậy nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.

Bài 3.43 trang 74 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2 AB.

a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?

b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.

Phương pháp:

a) Tứ giác BPCD có cặp cạnh đối song song và bằng nhau nên BPCD là hình bình hành.

b) Sử dụng tính chất của tam giác vuông cân và tia phân giác để tìm số đo các góc của tứ giác BPCD.

Lời giải: 

Bài 3.44 trang 74 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.59)

a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau

b) Chứng minh tứ giác APMN là một hình chữ nhật. Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC

c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh rằng tứ giác AMCQ là một hình thoi

d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?

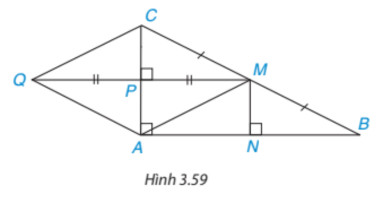
Phương pháp:

a) Chứng minh:  ΔCMP=ΔMBN (cạnh huyền – góc nhọn) 

b) Chứng minh APMN có ba góc vuông nên là hình chữ nhật, dựa vào tính chất của của hình chữ nhật suy ra các cặp cạnh song song, suy ra N, P là trung điểm của AB, AC.

c) Chứng minh AMCQ có hai đường chéo vuông góc với nhau.

d) Chứng minh hình thoi AMCQ có \(\widehat {AMC} = {90^o}\) nên AMCQ là hình vuông.

Lời giải: 

a) Ta có MP⊥AC, AB⊥AC suy ra MP//AB nên \(\widehat {CMP} = \widehat B\)

Xét tam giác vuông CMP và MBN ta có:

CM = MB (gt)

\(\widehat {CMP} = \widehat B\)

Suy ra ΔCMP=ΔMBN (cạnh huyền – góc nhọn) 

b) Xét tứ giác APMN có \(\widehat P = \widehat A = \widehat N = {90^o}\)suy ra APMN là hình chữ nhật

Xét tam giác ABC có: M là trung điểm AB, MP//AB suy ra P là trung điểm AC

Tương tự ta có: M là trung điểm AB, MN//AC suy ra N là trung điểm AB

c) Xét tứ giác AMCQ có: P là trung điểm MQ, P là trung điểm AC, AC⊥MQ suy ra AMCQ là hình thoi

d) Nếu ABC vuông cân tại A , AM là đường trung tuyến suy ra AM cũng là đường cao suy ra\(\widehat {AMC} = {90^o}\)

Xét hình thoi AMCQ có \(\widehat {AMC} = {90^o}\)suy ra AMCQ là hình vuông

Bài 3.45 trang 75 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E và K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N là chân đường vuông góc hạ từ B xuống ME (H.3.60)

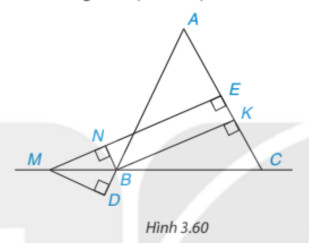
Chứng minh rằng:

a) Tứ giác BKEN là hình chữ nhật

b) BK và NE cùng bằng hiệu khoảng cách từ M đến AC và AB (dù M thay đổi trên đường thẳng MC miễn là B nằm giữa M và C)

Phương pháp:

a) Tứ giác BKEN có ba góc bằng 90^o 

b) Chứng minh ΔMBD = ΔMBN (cạnh huyền – góc nhọn)

Suy ra MD = MN

Lại có: BK = NE = ME – MN suy ra BK = NE = ME − MD.

Lời giải: 

Giaibaitap.me