Bài 1 trang 126 SGK Toán 8 Kết nối tri thức tập 2

Xây dựng công thức của hàm chi phí

Chi phí sử dụng truyền hình cáp của hai công ty dịch vụ truyền hình A và B như sau:

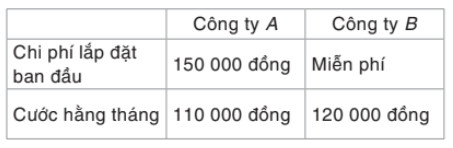
a) Viết công thức tính chi phí sử dụng truyền hình cáp y (nghìn đồng) của mỗi công ty A và B theo số tháng sử dụng là x (tháng)

b) Tính chi phí sử dụng truyền hình cáp trong 18 tháng của mỗi công ty A và B.

c) Với bao nhiêu tháng sử dụng thì chi phí sử dụng truyền hình cáp của hai công ty này là như nhau?

d) Vẽ đồ thị của hai hàm số nhận được ở câu a trên cùng một hệ trục tọa độ. Từ đó hãy cho biết nếu một gia đình dự định dùng một dịch vụ truyền hình cáp trong 3 năm thì nên chọn dịch vụ của công ty A hay công ty B để tiết kiệm chi phí hơn (giả sử chất lượng dịch vụ truyền hình cáp của hai công ty này là như nhau)

Lời giải:

a) Với số tháng sử dụng là x tháng. Ta có:

Công thức tính chi phí sử dụng truyền hình cáp công ty A là

y(A) = 110x + 150 (nghìn đồng).

Công thức tính chi phí sử dụng truyền hình cáp công ty B là

y(B) = 120x (nghìn đồng).

b) Chi phí sử dụng truyền hình cáp của công ty A trong 18 tháng là:

y(A18) = 110 . 18 + 150 = 2 130 (nghìn đồng).

Chi phí sử dụng truyền hình cáp của công ty B trong 18 tháng là:

y(B18) = 120 . 18 = 2 160 (nghìn đồng).

c) Ta có: 110x + 150 = 120x, suy ra x = 15.

Vậy sau 15 tháng sử dụng thì chi phí sử dụng truyền hình cáp của hai công ty là như nhau.

d) Vẽ các đồ thị y = 110x + 150 và y = 120x trên cùng một hệ trục tọa độ:

Đồ thị hàm số y = 110x + 150 là một phần đường thẳng đi điểm (0; 150) và (1; 260).

Đồ thị hàm số y = 120x là một phần đường thẳng đi qua gốc tọa độ O và đi qua (1; 120).

Số tháng sử dụng x và chi phí y tương ứng là các số không âm nên ta có các đồ thị trên được vẽ như hình dưới đây.

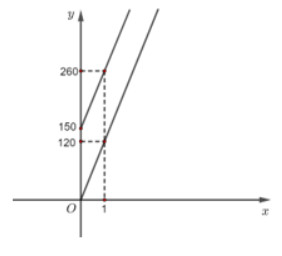
(Chia khoảng đơn vị trên 2 trục Ox và Oy là khác nhau).

Nếu lựa chọn dịch vụ sử dụng trong 3 năm thì nên chọn công ty A tiết kiệm chi phí hơn công ty B.

Bài 2 trang 126 SGK Toán 8 Kết nối tri thức tập 2

Giả sử rằng một hãng taxi vừa mua một số ô tô để chạy dịch vụ với chi phí là 480 triệu đồng một chiếc. Công ty chọn khấu hao theo đường thẳng trong vòng 8 năm. Điều này có nghĩa là mỗi chiếc xe sẽ giám giá 480 : 8 = 60 triệu đồng mỗi năm.

a) Tính giá trị sổ sách y(triệu đồng) của mỗi chiếc ô tô dưới dạng một hàm số bậc nhất của thời gian sử dụng x (năm) của nó.

b) Vẽ đồ thị của hàm số bậc nhất.

c) Giá trị sổ sách của mỗi chiếc ô tô sau 3 năm sử dụng là bao nhiêu?

d) Sau bao lâu thì giá trị sổ sách của mỗi chiếc ô tô còn lại là 150 triệu đồng?

Lời giải:

a) Giá trị sổ sách của mỗi chiếc ô tô sau x năm là: y = 480 – 60. x = - 60x + 480(triệu đồng)

b) Để vẽ đồ thị hàm số y = - 60x + 480 ta lấy hai điểm A(0; 480), B(1; 420). Đường thẳng AB chính là đồ thị hàm số y = - 60x + 480.

Ta có đồ thị hàm số như sau:

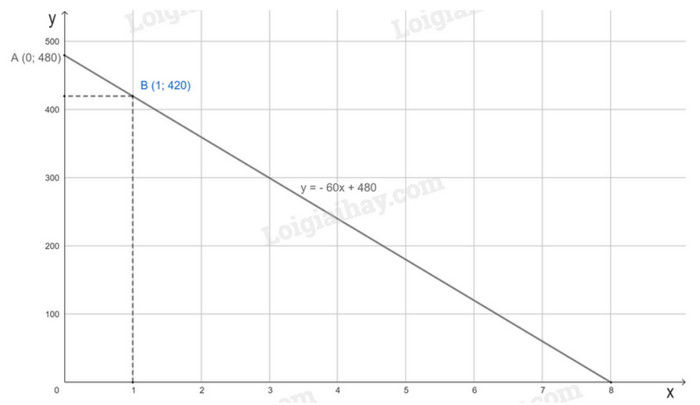
c) Giá trị sổ sách của ô tô sau 3 năm sử dụng là: y = – 60 . 3 + 450  = 300 (triệu đồng)

d) Ta có: – 60 . x + 480 = 150 suy ra: x = 5,5

Vậy sau 5,5 năm giá trị của sổ sách của ô tô còn lại 150 triệu đồng

Bài 3 trang 127 SGK Toán 8 Kết nối tri thức tập 2

Bác An dự định mua một chiếc tủ lạnh loại 150 lít của hãng A, có sông suất 1Kwh/ngày với giá 5 000 000 đồng và dự định sẽ sử dụng nó trong vòng 10 năm.

a) Giả sử trong quá trình một tháng có 30 ngày và giá điện là 2000 đồng/1Kwh. Hãy tính số tiền điện phải trả hằng tháng cho chiếc tủ lạnh này.

b) Giả sử trong quá trình sử dụng, tủ lạnh không bị hỏng hóc cần sửa chữa gì. Khi đó chi phí sử dụng tủ lạnh bao gồm chi phí mua ban đầu và chi phí trả tiền điện hằng tháng. Lập công thức tính chi phí sử dụng chiếc tủ lạnh này sau x (tháng)

c) Sử dụng công thức đã lập ở câu b, hãy tính chi phí sử dụng của tủ lạnh sau 5 năm.

d) Bác An dùng phương pháp khấu hao đường thẳng để tính giá trị còn lại của chiếc tủ lạnh sau mỗi năm sử dụng. Hỏi sau 7 năm giá trị còn lại của chiếc tủ lạnh này là bao nhiêu?

e) Hãng B cùng một loại tủ lạnh 150 lít, công suất 1,25Kwh/ ngày với giá bán là 4 460 000 đồng.

- Lập công thức tính chi phí sử dụng chiếc tủ lạnh của hãng B sau x (tháng)

- Sau bao nhiêu tháng sử dụng thì chi phí sử dụng của hai loại tủ lạnh này là bằng nhau?

- Vẽ đồ thị của hai hàm số chi phí sử dụng của hai loại tủ lạnh trên cùng một hệ trục tọa độ. Từ đồ thị đã vẽ, theo em bác An nên mua tủ lạnh của hãng A hay hãng B để tiết kiệm chi phí sử dụng hơn? (Giả sử bác An sẽ sử dụng trong vòng 10 năm và chất lượng của hai loại tủ lạnh là tương đương).

Lời giải:

a) Số tiền điện phải trả hàng tháng của chiếc tủ lạnh hãng A là: 2 000 . 30 = 60 000 (đồng).

b) Chi phí sử dụng của chiếc tủ lạnh hãng A sau x tháng là:

y = 5 000 000 + 60 000x (đồng).

c) Chi phí sử dụng của chiếc tủ lạnh hãng A sau 5 năm (60 tháng) là:

y(5) = 5 000 000 + 60 000 . 60 = 8 600 000 (đồng).

d) Sử dụng chiếc tủ lạnh trong 10 năm nên mỗi năm chiếc tủ lạnh sẽ giảm

5 000 000 : 10 = 500 000 (đồng).

Giá trị còn lại của chiếc tủ lạnh sau 7 năm là:

5 000 000 – 500 000 . 7 = 1 500 000 (đồng).

e) Công thức tính chi phí sử dụng chiếc tủ lạnh của hãng B sau x tháng là:

y = 4 460 000 + 1,25 . 2 000 . 30 . x = 4 460 000 + 75 000x (đồng).

Ta có: 5 000 000 + 60 000x = 4 460 000 + 75 000x

Suy ra x = 36.

Vậy sau 36 tháng sử dụng thì chi phí sử dụng của hai loại tủ lạnh là bằng nhau.

- Vẽ đồ thị hai hàm số chi phí sử dụng của hai loại tủ lạnh trên cùng một hệ trục tọa độ:

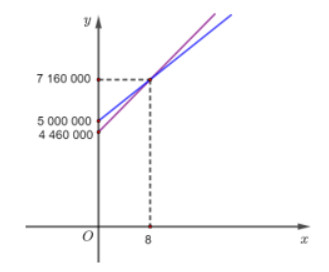
Như vậy, bác An nên sử dụng chiếc tủ lạnh của hãng A để tiết kiệm chi phí sử dụng.

Giaibaitap.me