Bài 4.13 trang 88 sách giáo khoa Toán 8 Kết nối tri thức tập 1

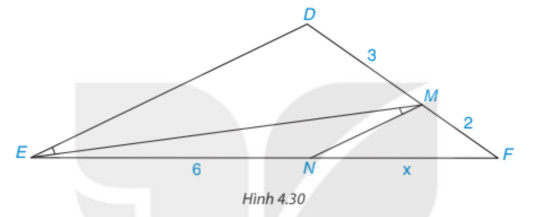
Tìm độ dài x trong Hình 4.30

Phương pháp:

Do MN //DE, áp dụng định lí Thalès ta có tỉ lệ thức để tính x.

Lời giải:

Bài 4.14 trang 88 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.

a) Chứng minh EK // CD, FK // AB.

b) So sánh EF và \(\dfrac{1}{2}(AB + C{\rm{D}})\)

Phương pháp:

a. Chứng minh EK là đường trung bình của tam giác ACD; FK là đường trung bình của tam giác ABC, suy ra EK // CD, FK // AB.

b. Áp dụng tính chất đường trung bình với EK và Fk trong tam giác ACD, ABC. Áp dụng bất đẳng thức tam giác vào tam giác KEF, suy ra đpcm.

Lời giải:

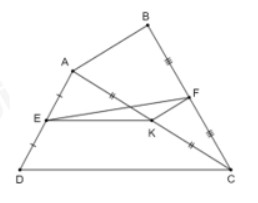
a) Vì E, K lần lượt là trung điểm của AD, AC nên EK là đường trung bình của tam giác ACD suy ra EK // CD.

Vì K, F lần lượt là trung điểm của AC, BC nên KF là đường trung bình của tam giác ABC suy ra KF // AB.

Vậy EK // CD, FK // AB.

b) Vì EK là đường trung bình của tam giác ACD nên \(EK = \dfrac{1}{2}C{\rm{D}}\);

Vì KF là đường trung bình của tam giác ABC nên \(KF = \dfrac{1}{2}AB\).

Do đó \(EK + KF = \dfrac{1}{2}(AB + C{\rm{D}})\)           (1)

Áp dụng bất đẳng thức tam giác vào tam giác KEF, ta có: \(EF \le EK + KF\)          (2)

Từ (1) và (2) ta suy ra \(EF \le \dfrac{1}{2}(AB + C{\rm{D}})\).

Bài 4.15 trang 88 sách giáo khoa Toán 8 Kết nối tri thức tập 1

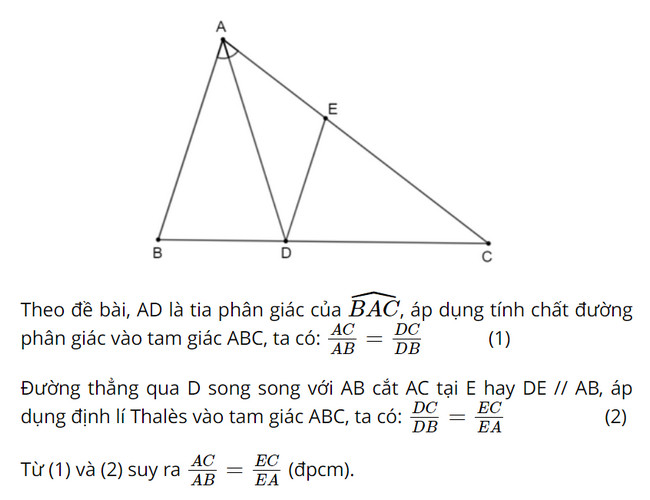
Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng \(\dfrac{{AC}}{{AB}} = \dfrac{{EC}}{{E{\rm{A}}}}\)

Phương pháp:

AD là tia phân giác của \(\widehat {BAC}\), áp dụng tính chất tia phân giác ta có được tỉ lệ thức. 

DE // AB, áp dụng định lí Thalès vào tam giác ABC, ta có tỉ lệ thức.

Từ đó suy ra đpcm.

Lời giải:

Bài 4.16 trang 88 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D.

a) Tính độ dài đoạn thẳng DB và DC.

b) Tính tỉ số diện tích của hai tam giác ABD và ACD.

Phương pháp:

a. AD là tia phân giác trong tam giác ABC, áp dụng tính chất đường phân giác của tam giác suy ra tỉ lệ thức, từ đó tính độ dài BD và CD.

b. Dựa vào công thức tính diện tích, ta tính được tỉ số diện tích hai tam giác ABD và ACD.

Lời giải: 

a) Áp dụng tính chất đường phân giác, ta có:

\(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}} = \dfrac{{15}}{{20}} = \dfrac{3}{4}\)

Suy ra \(\dfrac{{DB}}{3} = \dfrac{{DC}}{4}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{{DB}}{3} = \dfrac{{DC}}{4} = \dfrac{{DB + DC}}{{3 + 4}} = \dfrac{{BC}}{7} = \dfrac{{75}}{7}\)

Do đó, \(DB = \dfrac{{25.3}}{7} = \dfrac{{75}}{7}\) (cm).

Vậy \(DB = \dfrac{{75}}{7}cm;DC = \dfrac{{100}}{7}cm\) cm.

b)

Hai tam giác ABD và ACD có chung đường cao kẻ từ đỉnh A đến cạnh BC, ta gọi đường cao đó là AH.

Ta có: \({S_{AB{\rm{D}}}} = \dfrac{1}{2}AH.DB;{S_{A{\rm{D}}C}} = \dfrac{1}{2}AH.DC\)

Suy ra \(\dfrac{{{S_{AB{\rm{D}}}}}}{{{S_{A{\rm{D}}C}}}} = \dfrac{{\dfrac{1}{2}AH.B{\rm{D}}}}{{\dfrac{1}{2}AH.DC}} = \dfrac{{B{\rm{D}}}}{{DC}} = \dfrac{3}{4}\)

Vậy tỉ số diện tích của hai tam giác ABD và ACD bằng \(\dfrac{3}{4}\)

Bài 4.17 trang 88 sách giáo khoa Toán 8 Kết nối tri thức tập 1

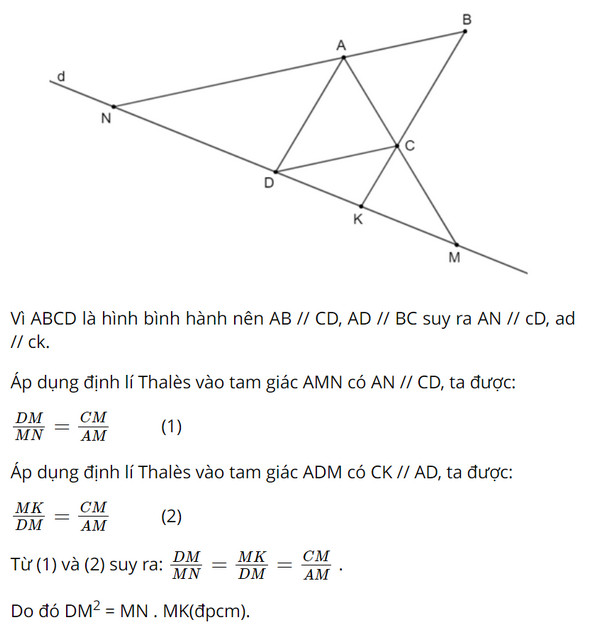
Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: \(D{M^2}\) = MN . MK.

Phương pháp:

Áp dụng định lí Thalès cho AN // CD, CK // AD, ta có các tỉ lệ thức. Từ đó ta suy ra đpcm.

Lời giải: 

Giaibaitap.me