A. SỐ HỌC VÀ ĐẠI SỐ

Bài 1 trang 135 SGK Toán 8 Kết nối tri thức tập 2

Thực hiện phép tính:

\(a){\left( {2{\rm{x}} + y} \right)^2} + {\left( {5{\rm{x}} - y} \right)^2} + 2\left( {2{\rm{x}} + y} \right)\left( {5{\rm{x}} - y} \right)\)

\(b)\left( {2{\rm{x}} - {y^3}} \right)\left( {2{\rm{x}} + {y^3}} \right) - \left( {2{\rm{x}} - {y^2}} \right)\left( {4{{\rm{x}}^2} + 2{\rm{x}}{y^2} + {y^4}} \right)\)

Lời giải:

\(\begin{array}{l}a){\left( {2{\rm{x}} + y} \right)^2} + {\left( {5{\rm{x}} - y} \right)^2} + 2\left( {2{\rm{x}} + y} \right)\left( {5{\rm{x}} - y} \right)\\ = 4{{\rm{x}}^2} + 4{\rm{x}}y + {y^2} + 25{{\rm{x}}^2} - 10{\rm{x}}y + {y^2} + 2.\left( {10{{\rm{x}}^2} - 2{\rm{x}}y + 5{\rm{x}}y - {y^2}} \right)\\ = 4{{\rm{x}}^2} + 4{\rm{x}}y + {y^2} + 25{{\rm{x}}^2} - 10{\rm{x}}y + {y^2} + 20{{\rm{x}}^2} - 4{\rm{x}}y + 10xy - 2{y^2}\\ = 49{{\rm{x}}^2}\end{array}\)

\(\begin{array}{l}b)\left( {2{\rm{x}} - {y^3}} \right)\left( {2{\rm{x}} + {y^3}} \right) - \left( {2{\rm{x}} - {y^2}} \right)\left( {4{{\rm{x}}^2} + 2{\rm{x}}{y^2} + {y^4}} \right)\\ = 4{{\rm{x}}^2} - {y^6} - 8{{\rm{x}}^3} - 4{{\rm{x}}^2}{y^2} - 2{\rm{x}}{y^4} + 4{{\rm{x}}^2}{y^2} + 2{\rm{x}}{y^4} + {y^6}\\ =  - 8{{\rm{x}}^3} + 4{{\rm{x}}^2}\end{array}\)

Bài 2 trang 135 SGK Toán 8 Kết nối tri thức tập 2

Cho đa thức: \(P = {x^2} - {y^2} + 6{\rm{x}} + 9\)

a) Phân tích đa thức P thành nhân tử

b) Sử dụng kết quả của câu a để tìm thương của phép chia đa thức P cho x+y+3

Lời giải:

a) Ta có:

\(\begin{array}{l}P = {x^2} - {y^2} + 6{\rm{x}} + 9\\P = \left( {{x^2} + 6{\rm{x}} + 9} \right) - {y^2}\\P = {\left( {x + 3} \right)^2} - {y^2}\\P = \left( {x + 3 + y} \right)\left( {x + 3 - y} \right)\end{array}\)

b) Thương của phép chia đa thức P cho x + y + 3 là x + 3 - y

Bài 3 trang 135 SGK Toán 8 Kết nối tri thức tập 2

Cho đa thức: \(f(x) = {x^2} - 15{\rm{x}} + 56\)

a) Phân tích đa thức thành nhân tử.

b) Tìm x sao cho f(x) = 0

Lời giải:

a) Ta có:

\(\begin{array}{l}f(x) = {x^2} - 15{\rm{x}} + 56\\f(x) = {x^2} - 7{\rm{x}} - 8{\rm{x  +  }}56\\f(x) = \left( {{x^2} - 7{\rm{x}}} \right) - \left( {8{\rm{x}} - 56} \right)\\f(x) = x\left( {x - 7} \right) - 8\left( {x - 7} \right)\\f(x) = \left( {x - 7} \right)\left( {x - 8} \right)\end{array}\)

b) Có \(\begin{array}{l}\left( {x - 7} \right)\left( {x - 8} \right) = 0\\ \Rightarrow x = 7{;^{}}x = 8\end{array}\)

Bài 4 trang 135 SGK Toán 8 Kết nối tri thức tập 2

Cho phân thức \(P = \frac{{2{{\rm{x}}^3} + 6{{\rm{x}}^2}}}{{2{{\rm{x}}^3} - 18{\rm{x}}}}\)

a) Viết điều kiện xác định và rút gọn phân thức P

b) Có thể tính giá trị của P tại x = −3 được không? Vì sao

c) Tính giá trị của phân thức P tại x = 4

d) Với giá trị nguyên nào của x thì P nhận giá trị nguyên?

Lời giải:

a) Điều kiện xác định của phân thức là: \(2{{\rm{x}}^3} - 18x \ne 0 \Rightarrow 2x\left( {{x^2} - 9} \right) \ne 0 \Rightarrow 2x\left( {x - 3} \right)\left( {x + 3} \right) \ne 0 \Rightarrow x \ne 0; x \ne 3{;^{}}x \ne  - 3\).

Ta có

$P=\frac{2 x^3+6 x^2}{2 x^3-18 x}=\frac{2 x^2(x+3)}{2 x\left(x^2-9\right)}=\frac{x^2(x+3)}{x\left(x^2-9\right)}=\frac{x^2(x+3)}{x(x-3)(x+3)}=\frac{x}{x-3}$.

b) Không thể tính giá trị của P tại x = -3 vì không thỏa mãn điều kiện xác định ở câu a.

c) Thay x = 4 vào P ta được:

\(P = \frac{4}{4-3} = 4\)

d) Ta có thể viết \(P = \frac{x}{x-3} = \frac{x-3+3}{x-3} = 1 + \frac{3}{x-3}\). Điều này cho thấy: P chỉ nhận giá trị nguyên khi \(\frac{3}{x-3}\) nhận giá trị nguyên. Muốn vậy, x - 3 phải là ước của 3. Mà 3 chỉ có các ước là ±1 và ±3. Do đó chỉ có thể xảy ra các trường hợp sau:

x - 3 = 1, tức là x = 4, khi đó P = 4;

x - 3 = -1, tức là x = 2, khi đó P = -2;

x - 3 = -3, tức là x = 0, khi đó P = 0;

x - 3 = 3, tức là x = 6; khi đó P = 2.

Vậy các giá trị cần tìm của x là \( x \in \{0; 2; 4; 6\}\).

Bài 5 trang 135 SGK Toán 8 Kết nối tri thức tập 2

Cho biểu thức:

\(P = \left( {\frac{{x + y}}{{1 - xy}} + \frac{{x - y}}{{1 + xy}}} \right):\left(1 + \frac{{{x^2} + {y^2} + 2{{\rm{x}}^2}{y^2}}}{{1 - {x^2}{y^2}}}\right)\)

Trong đó x và y là hai biến thỏa mãn điều kiện \({x^2}{y^2} - 1 \ne 0\)

a) Tính tổng \(A = \frac{{x + y}}{{1 - xy}} + \frac{{x - y}}{{1 + xy}}\) và \(B = 1 + \frac{{{x^2} + {y^2} + 2{{\rm{x}}^2}{y^2}}}{{1 - {x^2}{y^2}}}\)

b) Từ kết quả câu a) hãy thu gọn P và giải thích tại sao giá trị của P không phụ thuộc vào giá trị của biến y.

c) Chứng minh đẳng thức: \(P = 1 - \frac{{{{\left( {1 - x} \right)}^2}}}{{1 - {x^2}}}\)

d) Sử dụng câu c) hãy tìm các giá trị của x và y sao cho P = 1

Lời giải:

a) Ta có:

\(\begin{array}{l}A = \frac{{x + y}}{{1 - xy}} + \frac{{x - y}}{{1 + xy}}\\A = \frac{{\left( {x + y} \right)\left( {1 + xy} \right) + \left( {x - y} \right)\left( {1 - xy} \right)}}{{1 - {x^2}{y^2}}}\\A = \frac{{x + {x^2}y + y + x{y^2} + x - {x^2}y - y + x{y^2}}}{{1 - {x^2}{y^2}}}\\A = \frac{{2{\rm{x}} + 2{\rm{x}}{y^2}}}{{1 - {x^2}{y^2}}}\\A = \frac{{2x\left( {1 + {y^2}} \right)}}{{1 - {x^2}{y^2}}}\end{array}\)

\(\begin{array}{l}B = 1 + \frac{{{x^2} + {y^2} + 2{{\rm{x}}^2}{y^2}}}{{1 - {x^2}{y^2}}}\\B = \frac{{1 - {x^2}{y^2} + {x^2} + {y^2} + 2{{\rm{x}}^2}{y^2}}}{{1 - {x^2}{y^2}}}\\B = \frac{{1 + {x^2} + {y^2} + {x^2}{y^2}}}{{1 - {x^2}{y^2}}} \\ B = \frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{1 - {x^2}{y^2}}}\end{array}\)

b) Từ hai kết quả trên, ta có:

\(\begin{array}{l}P = \left( {\frac{{x + y}}{{1 - xy}} + \frac{{x - y}}{{1 + xy}}} \right):\left(1 + \frac{{{x^2} + {y^2} + 2{{\rm{x}}^2}{y^2}}}{{1 - {x^2}{y^2}}}\right)\\\frac{{2x\left( {1 + {y^2}} \right)}}{{1 - {x^2}{y^2}}}:\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{1 - {x^2}{y^2}}}\\ = \frac{{2x\left( {1 + {y^2}} \right)}}{{1 - {x^2}{y^2}}}.\frac{{1 - {x^2}{y^2}}}{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}} = \frac{{2{\rm{x}}}}{{1 + {x^2}}}\left( * \right)\end{array}\)

Vậy giá trị của P không phụ thuộc vào giá trị của biến y.

c) Ta có:

\(\begin{array}{l}1 - \frac{{{{\left( {1 - x} \right)}^2}}}{{1 + {x^2}}}\\ = \frac{{1 + {x^2} - 1 + 2{\rm{x}} - {x^2}}}{{1 + {x^2}}}\\ = \frac{{2{\rm{x}}}}{{1 + {x^2}}} = P\end{array}\)

d) Ta có:

\(\begin{array}{l}1 - \frac{{{{\left( {1 - x} \right)}^2}}}{{1 + {x^2}}} = 1\\ \Rightarrow \frac{{{{\left( {1 - x} \right)}^2}}}{{1 + {x^2}}} = 0\\ \Rightarrow {\left( {1 - x} \right)^2} = 0\\ \Rightarrow 1 - x = 0\\ \Rightarrow x = 1\\\end{array}\)

Vậy x = 1.

Bài 6 trang 135 SGK Toán 8 Kết nối tri thức tập 2

Bảng giá cước của một hãng taxi như sau:

a) Tính số tiền taxi phải trả khi di chuyển 35 km

b) Lập công thức tính số tiền taxi y (đồng) phải trả khi di chuyển x kilômét, với 1 < x  ≤ 30. Từ đó tính số tiền taxi phải trả khi di chuyển 30 km

c) Nếu một người phải trả số tiền taxi là 268 400 đồng, hãy tính quãng đường người đó đã di chuyển bằng taxi

Lời giải:

a) Số tiền phải trả khi di chuyển 1 km đầu là 10 000 đồng.

Số tiền phải trả khi di chuyển 29 km tiếp theo là 29.13 600 = 394 400 đồng.

Số tiền phải trả khi di chuyển 5 km cuối là 5.11 000 = 55 000 đồng.

Vậy số tiền phải trả cho 35 km là:

10 000 + 394 400 + 55 000 = 459 400 (đồng).

b) Vì \(1 < x \le 30\) nên số tiền trả cho quãng đường x kilomet gồm 2 phần: Phần thứ nhất là giá mở của 10 000 đồng, phần thứ hai là trả cho quãng đường x – 1 km tiếp theo. Công thức tính cần tìm là 10 000 + (x – 1) 13 600, hay 13 600x –  3 600, với \(1 < x \le 30\). (*)

Áp dụng (*): Nếu người đó di chuyển 30 km thì số tiền phải trả là

13 600. 30 – 3 600 = 404 400 (đồng).

c) Do số tiền đã trả cho taxi là 268 400, ít hơn 404 400 đồng, nên quãng đường đã di chuyển không quá 30 km. Vậy để tính quãng đường này, ta có thể dùng công thức (*).

13 600x – 3 600 = 268 400, hay 13 600x = 268 400 + 3 600 = 272 200, tức là x = 272 000 : 13 600 = 20 (km). 

Bài 7 trang 136 SGK Toán 8 Kết nối tri thức tập 2

Với giá trị nào của m, đường thẳng y=mx+1 (m≠0)

a) Song song với đường thẳng y=3x

b) Cắt trục hoành tại điểm có hoành độ bằng -2

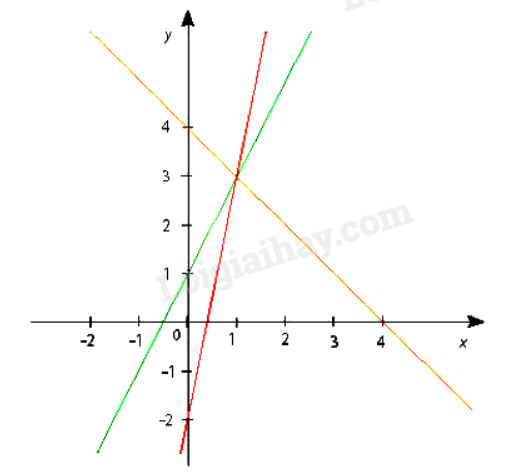
c) Đồng quy với các đường thẳng y=5x−2 và y=−x+4 (tức là ba đường thẳng này cắt nhau tại một điểm) Với giá trị m tìm được, hãy vẽ ba đường thẳng này trên cùng một hệ trục tọa độ để kiểm nghiệm kết quả.

Lời giải:

a) Hai đường thẳng cắt nhau khi a=a′ => m=3

b) Đường thẳng y = mx + 1 cắt trục hoành có hoành độ bằng -2

\(0 + 2m = 1 \Rightarrow m = \frac{1}{2}\)

c) Phương trình hoành độ giao điểm của đường thẳng y=−x+4 và y=5x−2 là

5x−2=−x+4

6x=6

x=1

Thay x=1 vào đường thẳng y=5x−2, có

y=5.1−2 => y=3

Thayx=1, y=3 vào đường thẳng y=mx+1 có

3=m+1 => m=2

B. HÌNH HỌC VÀ ĐO LƯỜNG

Bài 8 trang 136 SGK Toán 8 Kết nối tri thức tập 2

Cho hình bình hành ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi H là trung điểm của OB, K là trung điểm của OD

a) Hỏi tứ giác AHCK là hình gì?

b) Hình bình hành ABCD phải thỏa mãn điều kiện gì để tứ giác AHCK là:

- Một hình thoi

- Một hình chữ nhật

- Một hình vuông

Lời giải:

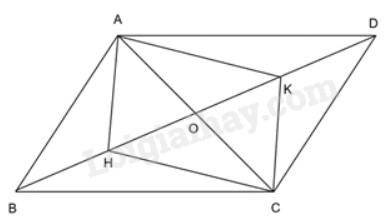
a) Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.

Do H và K lần lượt là trung điểm của OB và OD nên \(OH = \frac{{OB}}{2} = \frac{{OD}}{2} = OK\).

Các kết quả trên cho thấy tứ giác AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường. Vậy tứ giác AHCK là hình bình hành.

b)

Muốn tứ giác AHCK là hình thoi, ta cần thêm điều kiện hai đường chéo AC và HK vuông góc với nhau, cũng có nghĩa là AC \( \bot \) BD. Điều này xảy ra khi ABCD là hình thoi. Vậy điều kiện để tứ giác AHCK là hình thoi là tứ giác ABCD là hình thoi.

Muốn tứ giác AHCK là hình chữ nhật, ta cần thêm điều kiện hai đường chéo AC và HK bằng nhau, tức là AC = HK. Do H và K lần lượt là trung điểm của OB và OD nên điều kiện đó cũng có nghĩa là \(AC = \frac{1}{2}BD\). Vậy điều kiện để tứ giác AHCK là hình chữ nhật là ABCD có đường chéo BD dài gấp 2 lần đường chéo AC.

Tứ giác AHCK là hình vuông khi nó vừa là hình thoi, vừa là hình chữ nhật.

Do đó, theo kết quả hai câu trên, để AHCK là một hình vuông, thì hình bình hành ABCD phải là hình thoi, đường chéo BD dài gấp 2 lần đường chéo AC.

Bài 9 trang 136 SGK Toán 8 Kết nối tri thức tập 2

Cho tam giác ABC. Các đường trung tuyến AF, BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của BG và CG

a) Chứng minh rằng tứ giác DEKI là hình bình hành

b) Biết AF = 6cm. Tính độ dài các đoạn thẳng DI và EK

Lời giải:

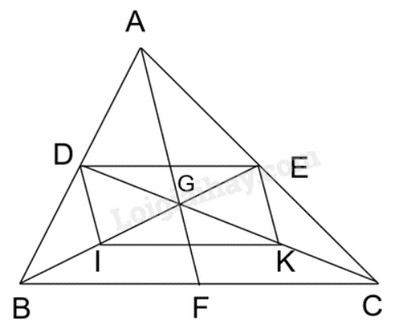
Xét tam giác ABC có:

D là đường trung tuyến của AB

E là đường trung tuyến của AC

=> DE là đường trung bình của tam giác ABC

=> DE // BC (1)

Tương tự, có IK là đường trung bình của tam giác GBC

=> IK // BC (2)

=> DE // IK (3)

- Có ID là đường trung bình của tam giác ABG => ID // AG

       EK là đường trung bình của tam giác ACG => EK // AG

=> ID // EK (4)

Từ (3) và (4) => DEIK là hình bình hành

b) Có điểm G là trọng tâm của tam giác ABC => \(AG = \frac{2}{3}{\rm{AF}}\)=> AG = 4cm

=> \(DI = EK = \frac{1}{2}AG = 2cm\)

Bài 10 trang 136 SGK Toán 8 Kết nối tri thức tập 2

Hình sau mô tả một dụng cụ đo bề dày (nhỏ hơn 1cm) của số sản phẩm. Dụng cụ này gồm một thướng AC = 10 cm, có vạch chia đến 1 mm, gắn với một bản kim loại có cạnh thẳng AB sao cho khoảng cách BC = 1cm.

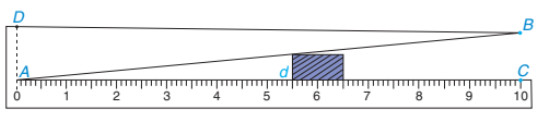
Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khhi đó trên thước ta đọc đường "bề dày" d của vật (trên hình vẽ ta có d = 5,5mm). Hãy giả thích tại sao với dụng cụ đó, ta có thể đo được bề dày d của các vật (với d < 10 mm)

Lời giải:

Kẹp vật vào giữa bản kim loại và thước như cách sử dụng đã mô tả; ta gọi B’C’ là đoạn ứng với bề dầy d cần đo của vât (nghĩa là d = B’C’). Dễ thấy B’C’ // BC vì cùng vuông góc với AC. Do đó $\Delta AB'C'\backsim \Delta ABC$, suy ra $\frac{B'C'}{BC}=\frac{A'C'}{AC}$.

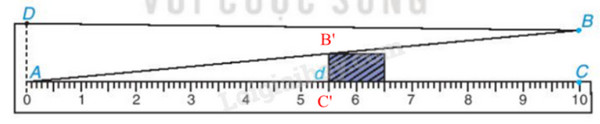
Do BC = 1 cm, AC = 10 cm nên đẳng thức này có nghĩa là B’C’ = $\frac{AC'}{10}$.

Vậy bề dày d của vật đúng bằng $\frac{1}{10}$ độ dài (cm) của AC’.

Chẳng hạn trên thức đo, AC’ = 5,5 cm có nghĩa là d = $\frac{5,5cm}{10}=5,5mm$.

Bài 11 trang 137 SGK Toán 8 Kết nối tri thức tập 2

Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I. Chứng minh rằng

a) ΔBIC \(\backsim\) ΔEIF

b) \(F{B^2} = FI.FC\)

c) Cho biết AB = 6cm, BC = 3 cm. Tính EF

Lời giải:

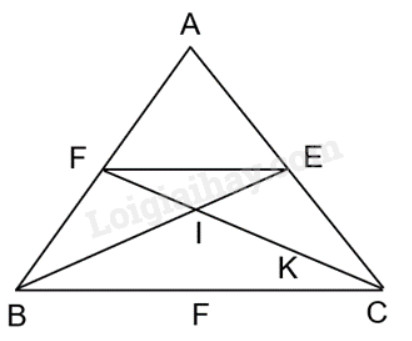
a) Vì tam giác ABC là tam giác cân

=> Hai đường phân giác đồng thời là đường trung tuyến

=> EF là đường trung bình của tam giác ABC

=> EF // BC

=> \(\widehat {IBC} = \widehat {IEF}{;^{}}\widehat {ICB} = \widehat {{\rm{IFE}}}\)(hai góc so le trong) 

=> ΔBIC \(\backsim\) ΔEIF (g.g)

b) Vì tam giác ABC cân tại A

=> \(\widehat {ABE} = \widehat {EBC} = \widehat {ACF} = \widehat {FCB}\)

Xét tam giác FBI và tam giác FCB có góc F chung, $\widehat{FBI}=\widehat{FCB}$

=> ΔFBI \(\backsim\) ΔFCB (g.g)

=> \(\frac{{FB}}{{FC}} = \frac{{FI}}{{FB}}\)

=> \(F{B^2} = FI.FC\)

c) Ta có EF // BC (chứng minh trên). Do đó:

\( \frac{BC}{EF} = \frac{AB}{AF} \Rightarrow \frac{ (AF + FB)}{AF} = 1 + \frac{BC}{AB}=1+ \frac{3}{6} = \frac{3}{2} \)

Từ đó suy ra \( EF = 3 : \frac{3}{2} = 2 \) (cm)

Bài 12 trang 137 SGK Toán 8 Kết nối tri thức tập 2

Cho tam giác ABC không phải là tam giác vuông, có các đường cao BE, CF cắt nhau tại điểm H

a) Giả sử ABC là tam giác nhọn. Chứng minh rằng ΔABE \(\backsim\) ΔACF , từ đó suy ra ΔAEF \(\backsim\) ΔABC

b) Cho biết AB = 10 cm, BC = 15 cm và BE = 8 cm. Tính EF 

Lời giải:

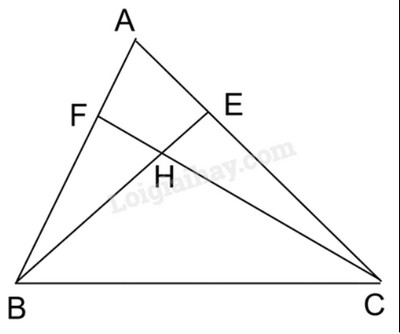
a) Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung => ΔABE \(\backsim\) ΔACF

=> \(\frac{{AB}}{{AC}} = \frac{{A{\rm{E}}}}{{AF}}\)

Xét tam giác AEF và tam giác ABC có: A chung và \(\frac{{AB}}{{AC}} = \frac{{A{\rm{E}}}}{{AF}}\)

=> ΔAEF \(\backsim\) ΔABC (c.g.c)

b) Xét tam giác vuông AEB có 

=> \(A{{\rm{E}}^2} = A{B^2} - B{E^2}\)

=> \(A{{\rm{E}}^2} = {10^2} - {8^2}\)

=> AE=6 cm

Vì ΔAEF \(\backsim\) ΔABC 

=> \(\frac{{A{\rm{E}}}}{{AB}} = \frac{{EF}}{{BC}}\)

=> \(\frac{6}{{10}} = \frac{{EF}}{{15}}\)

=> EF=9 cm

C. THỐNG KÊ VÀ XÁC SUẤT

Bài 13 trang 137 SGK Toán 8 Kết nối tri thức tập 2

Cho bảng thống kê sau:

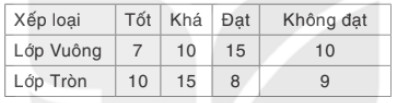
Để so sánh số lượng học sinh ở mỗi mức xếp loại của hai lớp ta nên dùng biểu đồ nào?

Lời giải:

Để so sánh số lượng học sinh ở mỗi mức xếp laoị của hai lớp ta nên dùng biểu đồ cột

Bài 14 trang 137 SGK Toán 8 Kết nối tri thức tập 2

Một túi đựng 24 viên bi giống hệt nhau và chỉ khác màu, trong đó có 9 viên bi màu đỏ, 6 viên bi màu xanh, 4 viên bi màu vàng và 5 viên bi màu đen. Bạn An lấy ngẫu nhiên một viên bi từ trong túi

a) Có bao nhiêu kết quả có thể? Các kết quả có thể này đồng khả năng không? Tại sao

b) Tính khả năng để xảy ra mỗi kết quả có thể đó

c) Tính xác suất để An lấy được:

- Viên bi màu vàng hoặc màu đỏ

- Viên bi màu đen hoặc màu xanh

- Viên bi không có màu đen

Lời giải:

a) Có 24 kết quả có thể của hành động trên. Do viên bi giống nhau nên 24 kết quả là đồng khả năng

b) Có 9 khả năng xảy ra lấy được viên bi màu đỏ,

- Có 6 khả năng xảy ra lấy được viên bi màu xanh.

- Có 4 khả năng xảy ra lấy được viên bi màu vàng.

- Có 5 khả năng lấy được viên bi màu đen.

Xác suất để An lấy được viên màu đỏ hoặc màu vàng là: \(\frac{{13}}{{24}}\)

Xác suất để An lấy được viên màu đen hoặc màu xanh là: \(\frac{{11}}{{24}}\)

Xác suất để An lấy được viên không có màu đen là: \(\frac{{19}}{{24}}\)

Giaibaitap.me