A. Trắc nghiệm

Bài 2.28 trang 47 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Đa thức \({x^2} - 9x + 8\) được phân tích thành tích của hai đa thức

A. \(x - 1\) và \(x + 8\)

B. \(x - 1\) và \(x - 8\)

C. \(x - 2\) và \(x - 4\)

D. \(x - 2\) và \(x + 4\)

Phương pháp:

Tách hạng tử -9x thành 2 hạng tử bậc 1 có tích các hệ số là 8, tổng bằng -9 rồi phân tích đa thức thành nhân tử bằng cách nhóm hạng tử. 

Lời giải:

\({x^2} - 9x + 8 = {x^2} - x - 8x + 8 = \left( {{x^2} - x} \right) - \left( {8x - 8} \right) = x\left( {x - 1} \right) - 8\left( {x - 1} \right) = \left( {x - 1} \right)\left( {x - 8} \right)\)

Chọn B.

Bài 2.29 trang 47 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Khẳng định nào sau đây là đúng?

A. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} + 2AB + {B^2}\)

B. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} - 2AB + {B^2}\)

C. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} + {B^2}\)

D. \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} - {B^2}\)

Phương pháp:

Sử dụng hằng đẳng thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\)

Lời giải: 

Đáp án đúng là: D

Ta có (A – B)(A + B) = (A + B)(A – B) = A² – B².

Bài 2.30 trang 47 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Biểu thức \(25{x^2} + 20xy + 4{y^2}\) viết dưới dạng bình phương của một tổng là:

A. \({\left[ {5x + \left( { - 2y} \right)} \right]^2}\)

B. \({\left[ {2x + \left( { - 5y} \right)} \right]^2}\)

C. \({\left( {2x + 5y} \right)^2}\)

D. \({\left( {5x + 2y} \right)^2}\).

Phương pháp:

Áp dụng hằng đẳng thức \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)

Lời giải: 

\(25{x^2} + 20xy + 4{y^2} = {\left( {5x} \right)^2} + 2.5x.2y + {\left( {2y} \right)^2} = {\left( {5x + 2y} \right)^2}\)

Chọn D.

Bài 2.31 trang 47 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Rút gọn  biểu thức \(A = {\left( {2x + 1} \right)^3} - 6x\left( {2x + 1} \right)\) ta được

A. \({x^3} + 8\)

B. \({x^3} + 1\)

C. \(8{x^3} + 1\)

D. \(8{x^3} - 1\)

Phương pháp:

Áp dụng hằng đẳng thức \({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\) và quy tắc nhân đơn thức với đa thức; cộng, trừ đa thức.

Lời giải: 

Đáp án đúng là: C

Ta có A = (2x + 1)³ – 6x(2x + 1)

= (2x)³ + 3 . (2x)² . 1 + 3 . 2x . 1² + 1³ – 12x² – 6x

= 8x³ + 12x² + 6x + 1 – 12x² – 6x = 8x³ + 1.

B. Tự luận

Bài 2.32 trang 47 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Tính nhanh giá trị của các biểu thức:

a) \({x^2} - 4x + 4\) tại x=102.

b) \({x^3} + 3{x^2} + 3x + 1\) tại x=999.

Phương pháp:

Sử dụng hằng đẳng thức để biến đổi biểu thức rồi thay các giá trị x vào biểu thức.

Lời giải: 

a) \({x^2} - 4x + 4 = {x^2} - 2.x.2 + {2^2} = {\left( {x - 2} \right)^2}\)

Thay \(x = 102\) vào biểu thức ta được \({\left( {102 - 2} \right)^2} = {100^2} = 10000\)

b) \({x^3} + 3{x^2} + 3x + 1 = {\left( {x + 1} \right)^3}\)

Thay x=999 vào biểu thức ta được \({\left( {999 + 1} \right)^3} = {1000^3} = 1000000000\)

Bài 2.33 trang 47 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Rút gọn các biểu thức:

a) \(\left( {2x - 5y} \right)\left( {2x + 5y} \right) + {\left( {2x + 5y} \right)^2}\)

b) \(\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right) + \left( {2x - y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)\)

Phương pháp:

a) Đặt nhân tử chung

b) Sử dụng hằng đẳng thức:

\({A^3} + {B^3} = \left( {A + B} \right)\left( {A - AB + {B^2}} \right)\)

\({A^3} - {B^3} = \left( {A - B} \right)\left( {A + AB + {B^2}} \right)\)

Lời giải: 

a) (2x – 5y)(2x + 5y) + (2x + 5y)²

= 4x² – 25y² + 4x² + 20xy + 25y²

= 8x² + 20xy.

b) (x + 2y)(x² – 2xy + 4y²) + (2x – y)(4x² + 2xy + y²)

= (x + 2y)[x² – x . 2y + (2y)²] + (2x – y)[(2x)² + 2x . y + y²]

= (x + 2y)[x² – x . 2y + (2y)²] + (2x – y)[(2x)² + 2x . y + y²]

= x³ + (2y)³ + (2x)³ – y³

= x³ + 8y³ + 8x³ – y³

= 9x³ + 7y³.

Bài 2.34 trang 47 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Phân tích các đa thức sau thành nhân tử:

a) \(6{x^2} - 24{y^2}\)

b) \(64{x^3} - 27{y^3}\)

c) \({x^4} - 2{x^3} + {x^2}\)

d) \({\left( {x - y} \right)^3} + 8{y^3}\)

Phương pháp:

Sử dụng phương pháp nhóm nhân tử chung, áp dụng các hằng đẳng thức:

\({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\)

\({A^3} + {B^3} = \left( {A + B} \right)\left( {A - AB + {B^2}} \right)\)

\({A^3} - {B^3} = \left( {A - B} \right)\left( {A + AB + {B^2}} \right)\)

Lời giải: 

a) \(6{x^2} - 24{y^2} = 6.\left( {{x^2} - 4{y^2}} \right) = 6\left[ {{x^2} - {{\left( {2y} \right)}^2}} \right] = 6\left( {x - 2y} \right)\left( {x + 2y} \right)\)

b) \(64{x^3} - 27{y^3} = {\left( {4x} \right)^3} - {\left( {3y} \right)^3} = \left( {4x - 3y} \right)\left[ {{{\left( {4x} \right)}^2} + 4x.3y + {{\left( {3y} \right)}^2}} \right] = \left( {4x - 3y} \right)\left( {16{x^2} + 12xy + 9{y^2}} \right)\)

c) \({x^4} - 2{x^3} + {x^2} = {x^2}.\left( {{x^2} - 2x + 1} \right) = {x^2}.{\left( {x - 1} \right)^2}\)

d)       

\(\begin{array}{l}{\left( {x - y} \right)^3} + 8{y^3} = {\left( {x - y} \right)^3} + {\left( {2y} \right)^3} = \left( {x - y + 2y} \right)\left[ {{{\left( {x - y} \right)}^2} - \left( {x - y} \right).2y + {{\left( {2y} \right)}^2}} \right]\\ = \left( {x + y} \right)\left( {{x^2} - 2xy + {y^2} - 2xy + 2{y^2} + 4{y^2}} \right)\\ = \left( {x + y} \right)\left( {{x^2} -4xy + 7{y^2}} \right)\end{array}\)

Bài 2.35 trang 47 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\).

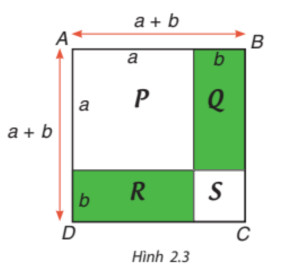
Phương pháp:

Cách 1: Diện tích hình vuông bằng bình phương một cạnh.

Cách 2: Diện tích ABCD = Diện tích P + Q + R + S

Lời giải: 

Cách 1. Tính diện tích hình vuông ABCD có độ dài một cạnh bằng a + b.

Diện tích hình vuông ABCD là: (a + b)²

Cách 2. Tính diện tích hình vuông ABCD bằng tổng diện tích các hình P, Q, R, S.

Diện tích hình vuông P là: a²;

Diện tích hình hình chữ nhật Q là: ab;

Diện tích hình hình chữ nhật R là: ab;

Diện tích hình vuông S là: b²;

Diện tích hình vuông ABCD là: a² + ab + ab + b² = a² + 2ab + b².

Từ hai cách tính diện tích hình vuông ABCD ở trên, ta có: (a + b)² = a² + 2ab + b².

Giaibaitap.me