Bài 3.4 trang 55 sách giáo khoa Toán 8 Kết nối tri thức tập 1

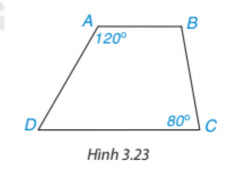
Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao

Phương pháp:

Áp dụng định lí tổng các góc trong một tứ giác bằng \(360^0\)

Lời giải:

Để hình thang ABCD là hình thang cân thì \(\widehat A = \widehat B = {120^o};\widehat C = \widehat D = {80^o}\)

Suy ra \(\widehat A + \widehat B + \widehat C + \widehat D\)=120°+120°+80°+80°=400°>360°(không thỏa mãn định lí tổng bốn góc trong một tứ giác).

Khi đó, ABCD không phải là tứ giác.

Do đó ABCD cũng không phải là hình thang cân.

Bài 3.5 trang 55 sách giáo khoa Toán 8 Kết nối tri thức tập 1

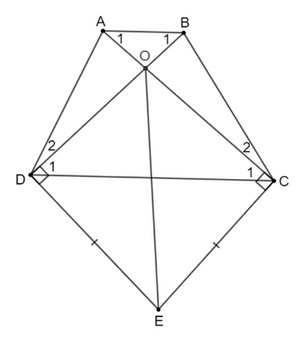
Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Phương pháp:

Gọi O là giao điểm của AC và BD.

Chứng minh hai đường chéo AC = BD nên ABCD là hình thang cân.

Lời giải:

Gọi O là giao điểm của AC và BD.

Xét ∆DOE và ∆COE có:

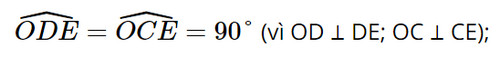
EC = ED (giả thiết);

Cạnh OE chung

Do đó ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).

Suy ra OC = OD (hai cạnh tương ứng) (1)

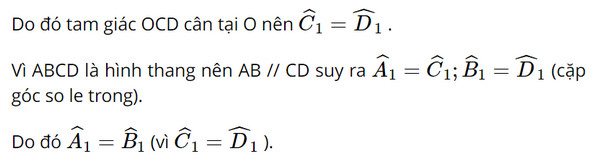
Suy ra tam giác OAB cân tại O nên OA = OB (2)

Ta có: AC = OA + OC và BD = OB + OD (3)

Từ (1), (2) và (3) suy ra AC = BD

Hình thang ABCD có AC = BD nên ABCD là hình thang cân.

Bài 3.6 trang 55 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Vẽ hình thang cân ABCD (AB // CD) biết đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm.

Phương pháp:

Vận dụng các tính chất của hình thang cân

+ Hai cạnh bên bằng nhau

+ Hai đường chéo bằng nhau

Sử dụng compa để vẽ hình

Lời giải:

Cách vẽ hình thang cân ABCD có đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm:

– Vẽ cạnh CD = 4 cm.

– Dùng compa vẽ hai đường tròn (D; 2 cm) và (C; 3 cm). Hai đường tròn này cắt nhau tại điểm A.

– Dùng compa vẽ hai đường tròn (D; 3 cm) và (C; 2 cm). Hai đường tròn này cắt nhau tại điểm B.

– Nối AB, AD, BC ta được hình thang cân ABCD (như hình vẽ). 

Bài 3.7 trang 55 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Phương pháp:

Chứng minh: ∆ADE = ∆BCE (g.c.g) suy ra EC = ED

Lời giải: 

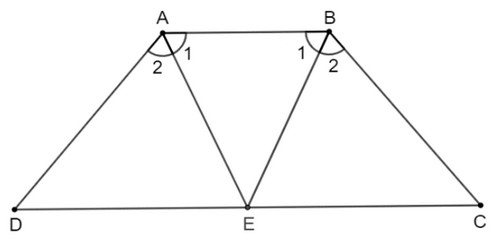
Vì ABCD là hình thang cân nên \(\widehat {DAB} = \widehat {ABC};\widehat C = \widehat D;A{\rm{D}} = BC\)

Theo đề bài, ta có AE, BE lần lượt là tia phân giác của \(\widehat {BA{\rm{D}}}\) và \(\widehat {ABC}\)

Suy ra \(\widehat {{A_1}} = \widehat {{A_2}};\widehat {{B_1}} = \widehat {{B_2}}\)

Mà \(\widehat {DAB} = \widehat {ABC}\) nên \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}}\)

Xét ∆ADE và ∆BCE có:

\(\widehat {{A_2}} = \widehat {{B_2}}\) (chứng minh trên)

AD = BC (chứng minh trên)

\(\widehat {{D}} = \widehat {{C}}\) (chứng minh trên)

Do đó ∆ADE = ∆BCE (g.c.g).

Suy ra EC = ED (hai cạnh tương ứng).

Bài 3.8 trang 55 sách giáo khoa Toán 8 Kết nối tri thức tập 1

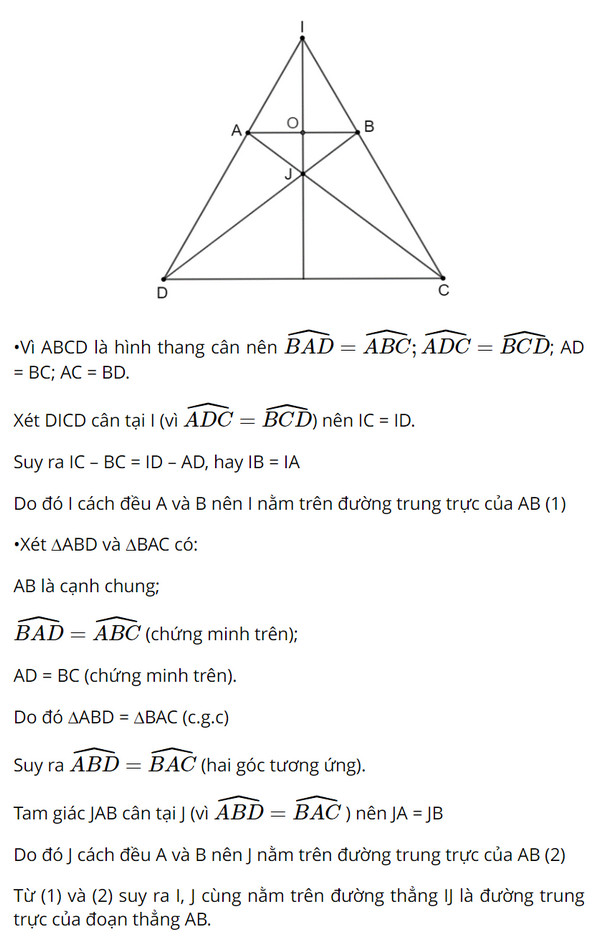
Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.

Phương pháp:

Gọi O là giao điểm của AB và IJ

Chứng minh: Tam giác IAB cân tại I (vì IA = IB) có IO là tia phân giác \(\widehat {AIB}\)

Suy ra IO là đường trung trực của đoạn thẳng AB.

Suy ra đường thẳng IJ là đường trung trực của đoạn thẳng AB

Lời giải: 

Giaibaitap.com