Bài 2.22 trang 44 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Phân tích các đa thức sau thành nhân tử:

\(\begin{array}{l}a)\,{x^2} + xy;\\b)\,6{a^2}b - 18ab;\\c)\,{x^3} - 4x;\\d)\,{x^4} - 8x.\end{array}\)

Phương pháp:

Sử dụng phương pháp đặt nhân tử chung và sử dụng hằng đẳng thức.

Lời giải:

\(\begin{array}{l}a)\,{x^2} + xy = x.x + x.y = x\left( {x + y} \right); \\b)\,6{a^2}b - 18ab = 6ab\left( {a - 3} \right); \\c)\,{x^3} - 4x = x\left( {{x^2} - 4} \right) = x\left( {x - 2} \right)\left( {x + 2} \right); \\d)\,{x^4} - 8x = x\left( {{x^3} - 8} \right) = x\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right).\end{array}\)

Bài 2.23 trang 44 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Phân tích các đa thức sau thành nhân tử:

a) \({x^2} - 9 + xy + 3y\)

b) \({x^2}y + {x^2} + xy - 1\)

Phương pháp:

Phân tích đa thức thành nhân tử bằng cách nhóm hạng tử, sử dụng hằng đẳng thức.

Lời giải:

a) x² – 9 + xy + 3y = (x² – 9) + (xy + 3y)

= (x + 3)(x – 3) + y(x + 3)

= (x + 3)(x + y – 3).

b) x²y + x² + xy – 1 = (x²y + xy) + (x² – 1)

= xy(x + 1) + (x + 1)(x – 1) = (x + 1)(xy + x – 1).

Bài 2.24 trang 44 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Tìm x biết:

a) \({x^2} - 4x = 0\)

b) \(2{x^3} - 2x = 0\)

Phương pháp:

Phân tích đa thức thành nhân tử.

\(A.B = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{A = 0}\\{B = 0}\end{array}} \right.\)

Lời giải:

a)

\(\begin{array}{l}{x^2} - 4x = 0\\ \Leftrightarrow x\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x - 4 = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 4}\end{array}} \right.\end{array}\)

Vậy \(x \in \left\{ {0;4} \right\}\)

b)

\(\begin{array}{l}2{x^3} - 2x = 0\\ \Leftrightarrow 2x\left( {{x^2} - 1} \right) = 0\\ \Leftrightarrow 2x\left( {x - 1} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 1 = 0\\x + 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x =  - 1\end{array} \right.\end{array}\)

Vậy \(x \in \left\{ {0;1; - 1} \right\}\)

Bài 2.25 trang 44 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2)

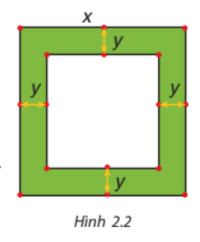
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.

b) Phân tích S thành nhân tử rồi tính A khi x=102 m, y=2 m.

Phương pháp:

Viết biểu thức.

Diện tích đường bao quanh = diện tích mảnh vườn hình vuông – diện tích bên trong vườn.

Phân tích đa thức thành nhân tử.

Lời giải: 

a) Đặt tên các điểm A, B, C, D, M, N, P, Q như hình vẽ.

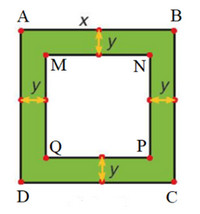
Diện tích hình vuông ABCD là: x² (m).

Hình vuông MNPQ có độ dài một cạnh là: x – y – y = x – 2y (m).

Diện tích hình vuông MNPQ là: (x – 2y)² (m²).

Diện tích S của đường bao quanh mảnh vườn là:

S = x² – (x – 2y)² = x² – (x² – 4xy + 4y²)

= x² – x² + 4xy – 4y² = 4xy – 4y² (m²).

Vậy diện tích S của đường bao quanh mảnh vườn là 4xy – 4y² (m²).

b) Phân tích đa thức S thành nhân tử, ta được:

S = 4xy – 4y² = 4y(x – y).

Thay x = 102 m, y = 2 m vào biểu thức S, ta được:

S = 4 . 2 . (102 – 2) = 8 . 100 = 800 (m²).

Giaibaitap.me