Bài 1.8 trang 14 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Trong các biểu thức sau, biểu thức nào là đa thức?

\( - {x^2} + 3x + 1;\dfrac{x}{{\sqrt 5 }};x - \dfrac{{\sqrt 5 }}{x};2024;3{x^2}{y^2} - 5{x^3}y + 2,4;\dfrac{1}{{{x^2} + x + 1}}.\)

Phương pháp:

Đa thức là tổng của những đơn thức; mỗi đơn thức trong tổng được gọi là một hạng tử của đa thức đó.

Lời giải:

Các đa thức là: \( - {x^2} + 3x + 1;\dfrac{x}{{\sqrt 5 }};2024;3{x^2}{y^2} - 5{x^3}y + 2,4.\)

Bài 1.9 trang 14 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Xác định hệ số và bậc của từng hạng tử trong đa thức sau:

a) \({x^2}y - 3xy + 5{x^2}{y^2} + 0,5x - 4\)

b) (x\sqrt 2  - 2x{y^3} + {y^3} - 7{x^3}y\)

Phương pháp:

+) Hệ số là phần số.

+) Bậc của đơn thức là tổng lũy thừa của các biến trong đơn thức.

Lời giải:

a) Đa thức x²y – 3xy + 5x²y² + 0,5x – 4 có:

- Hạng tử x²y có hệ số là 1, bậc là 3;

- Hạng tử –3xy có hệ số là –3, bậc là 2;

- Hạng tử 5x²y² có hệ số là 5, bậc là 4;

- Hạng tử 0,5x có hệ số là 0,5, bậc là 1;

- Hạng tử –4 có hệ số là –4, bậc là 0.

b)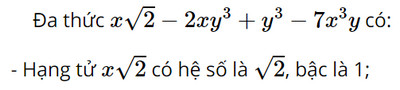 

- Hạng tử −2xy³ có hệ số là −2, bậc là 4;

- Hạng tử y³ có hệ số là 1, bậc là 3;

- Hạng tử −7x³y có hệ số là −7, bậc là 4.

Bài 1.10 trang 14 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Thu gọn đa thức:

a) \(5{x^4} - 2{x^3}y + 20x{y^3} + 6{x^3}y - 3{x^2}{y^2} + x{y^3} - {y^4}\)

b) \(0,6{x^3} + {x^2}z - 2,7x{y^2} + 0,4{x^3} + 1,7x{y^2}\)

Phương pháp:

Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.

Lời giải:

a)

\(\begin{array}{l}5{x^4} - 2{x^3}y + 20x{y^3} + 6{x^3}y - 3{x^2}{y^2} + x{y^3} - {y^4}\\ = 5{x^4} + \left( { - 2{x^3}y + 6{x^3}y} \right) - 3{x^2}{y^2} + \left( {20x{y^3} + x{y^3}} \right) - {y^4}\\ = 5{x^4} + 4{x^3}y - 3{x^2}{y^2} + 21x{y^3} - {y^4}\end{array}\)

Bậc của đa thức là: 4

b)

\(\begin{array}{l}0,6{x^3} + {x^2}z - 2,7x{y^2} + 0,4{x^3} + 1,7x{y^2}\\ = \left( {0,6{x^3} + 0,4{x^3}} \right) + {x^2}z + \left( { - 2,7x{y^2} + 1,7x{y^2}} \right)\\ = {x^3} + {x^2}z - x{y^2}\end{array}\)

Bậc của đa thức là: 3

Bài 1.11 trang 14 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Thu gọn (nếu cần) và tìm bậc của mỗi đa thức sau:

a) \({x^4} - 3{x^2}{y^2} + 3x{y^2} - {x^4} + 1\)

b) \(5{x^2}y + 8xy - 2{x^2} - 5{x^2}y + {x^2}\)

Phương pháp:

Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.

Lời giải: 

a) Thu gọn đa thức:

x⁴ – 3x²y² + 3xy² – x⁴ + 1

= (x⁴ – x⁴) – 3x²y² + 3xy² + 1

= – 3x²y² + 3xy² + 1.

Đa thức thu gọn ở trên có bậc là 4 nên đa thức đã cho có bậc là 4.

b) Ta có: 5x²y + 8xy – 2x² – 5x²y + x²

= (5x²y – 5x²y) + 8xy + (x²– 2x²) = 8xy – x².

Đa thức 8xy – x² có bậc là 2 nên đa thức 5x²y + 8xy – 2x² – 5x²y + x² có bậc là 2.

Bài 1.12 trang 14 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Thu gọn rồi tính giá trị của đa thức:

\(M = \dfrac{1}{3}{x^2}y + x{y^2} - xy + \dfrac{1}{2}x{y^2} - 5xy - \dfrac{1}{3}{x^2}y\) tại x=0,5 và y=1.

Phương pháp:

Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.

Thay các giá trị x=0,5 và y=1 vào đa thức M rồi tính giá trị.

Lời giải: 

\(\begin{array}{l}M = \dfrac{1}{3}{x^2}y + x{y^2} - xy + \dfrac{1}{2}x{y^2} - 5xy - \dfrac{1}{3}{x^2}y\\ = \left( {\dfrac{1}{3}{x^2}y - \dfrac{1}{3}{x^2}y} \right) + \left( {x{y^2} + \dfrac{1}{2}x{y^2}} \right) + \left( { - xy - 5xy} \right)\\ = \dfrac{3}{2}x{y^2} - 6xy\end{array}\)

Thay x=0,5 và y=1 vào M ta được:

\(M = \dfrac{3}{2}.0,{5.1^2} - 6.0,5.1 =  - 2,25.\)

Bài 1.13 trang 14 sách giáo khoa Toán 8 Kết nối tri thức tập 1

Cho đa thức \(P = 8{x^2}{y^2}z - 2xyz + 5{y^2}z - 5{x^2}{y^2}z + {x^2}{y^2} - 3{x^2}{y^2}z.\)

a) Thu gọn và tìm bậc của đa thức P;

b) Tính giá trị của đa thức P tại x=-4;y=2 và z=1.

Phương pháp:

a) Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.

Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.

b) Thay các giá trị x=-4;y=2 và z=1 vào đa thức P rồi tính giá trị.

Lời giải: 

a) Ta có: P = 8x²y²z – 2xyz + 5y²z – 5x²y²z + x²y² – 3x²y²z

= (8x²y²z – 3x²y²z– 5x²y²z) + x²y²– 2xyz + 5y²z

= x²y²– 2xyz + 5y²z.

b) Thay x = –4; y = 2 và z = 1 vào đa thức P, ta được:

P = (–4)² . 2²– 2 . (–4) . 2 . 1 + 5 . 2² . 1 = 16 . 4 + 8 . 2 + 5 . 4

= 64 + 16 + 20 = 100.

Vậy P = 100 tại x = –4; y = 2 và z = 1.

Giaibaitap.me