Bài tập trắc nghiệm khách quan
Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án cho để được khẳng đinh đúng.
80. Hàm số \(f\left( x \right) = {{{x^3}} \over 3} - {{{x^2}} \over 2} - 6x + {3 \over 4}\)
(A) Đồng biến trên khoảng \(\left( { - 2;3} \right)\)
(B) Nghịch biến trên khoảng \(\left( { - 2;3} \right)\)
(C) Nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\)
(D) Đồng biến trên khoảng \(\left( { - 2; + \infty } \right)\)
Giải
\(f'\left( x \right) = {x^2} - x - 6;\,\,f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 3 \hfill \cr} \right.\)
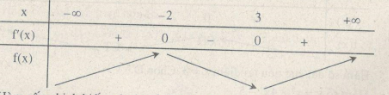
(B) Nghịch biến trên khoảng \(\left( { - 2;3} \right)\). Chọn (B).
81. Hàm số \(f\left( x \right) = 6{x^5} - 15{x^4} + 10{x^3} - 22\)
(A) Nghịch biến trên R;
(B) Đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\);
(C) Đồng biến trên khoảng R;
(D) Nghịch biến trên khoảng (0;1).
Giải
\(\eqalign{
& f'\left( x \right) = 30{x^4} - 60{x^3} + 30{x^2} \cr&= 30{x^2}\left( {{x^2} - 2x + 1} \right) \cr&= 30{x^2}{\left( {x - 1} \right)^2} \ge 0 \cr
& f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr} \right. \cr} \)
Hàm số đồng biến trên R. Chọn C.
82. Hàm số \(y = \sin x - x\)
(A) Đồng biến trên R.
(B) Đồng biến trên khoảng \(\left( { - \infty ;0} \right)\)
(C) Nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
(D) Nghịch biến trên R.
Giải
\(y' = \cos x - 1 \le 0\,\,\,\,\,\forall x \in R\). Dấu bằng xảy ra khi và chỉ khi \(x = 2k\pi \)
Hàm số nghịch biến trên R. Chọn D.
83. Hàm số \(f\left( x \right) = {x^3} - 3{x^2} - 9x + 11\)
(A) Nhận điểm x = -1 làm điểm cực tiểu;
(B) Nhận điểm x = 3 làm điểm cực đại;
(C) Nhận điểm x = 1 làm điểm cực đại;
(D) Nhận điểm x = 3 làm điểm cực tiểu.
Giải
\(\eqalign{
& f'\left( x \right) = 3{x^2} - 6x - 9 \cr
& f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
x = 3 \hfill \cr} \right. \cr} \)
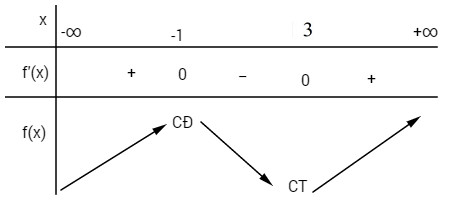
Hàm số đạt cực tiểu tại điểm x = 3. Chọn D.
Giaibaitap.me
Giải bài tập trang 64, 65, 66, 67 ôn tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số SGK Giải tích 12 Nâng cao. Câu 84: Hàm số ...
Giải bài tập trang 66 ôn tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số SGK Giải tích 12 Nâng cao. Câu 92: Giá trị lớn nhất của hàm số...
Giải bài tập trang 64, 65, 66, 67 ôn tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số SGK Giải tích 12 Nâng cao. Câu 97: Xét phương trình...
Giải bài tập trang 75, 76 bài 1 lũy thừa với số mũ hữu tỉ SGK Giải tích 12 Nâng cao. Câu 1: Trong các khẳng định sau, khẳng định nào đúng...
