Bài 23 trang 199 SGK Đại số và Giải tích 12 Nâng cao

Tìm nghiệm phức phương trình \(z + {1 \over z} = k\) trong các trường hợp sau:

a) \(k = 1\);                

b) \(k = \sqrt 2 \)                       

c) \(k = 2i\)

Giải

 \(z + {1 \over z} = k\)

Ta có \(z + {1 \over z} = k \Leftrightarrow {z^2} - kz + 1 = 0\)

Phương trình có hai nghiệm là \(z = {{k \pm \delta } \over 2}\) trong đó \(\delta \) là một căn bậc hai của \(\Delta  = {k^2} - 4\)

a) Với \(k = 1\) thì \(\Delta  =  - 3\) khi đó \(z = {{1 \pm \sqrt 3 i} \over 2}\)

b) Với \(k = \sqrt 2 \) thì \(\Delta  =  - 2\) khi đó \(z = {{\sqrt 2  \pm \sqrt 2 i} \over 2}\)\( = {{\sqrt 2 } \over 2}\left( {1 \pm i} \right)\)

c) Với \(k = 2i\) thì \(\Delta  =  - 8\) khi đó \(z = {{2i \pm 2\sqrt 2 i} \over 2} = \left( {1 \pm \sqrt 2 } \right)i\)

Bài 24 trang 199 SGK Đại số và Giải tích 12 Nâng cao

Giải các phương trình sau trên C và biểu diễn hình hợp tập hợp các nghiệm của mỗi phương trình (trong mặt phẳng phức):

a)\({z^3} + 1 = 0\);                                               

b) \({z^4} - 1 = 0\);

c) \({z^4} + 4 = 0\);                                          

d) \(8{z^4} + 8{z^3} = z + 1\).

Giải

a) \({z^3} + 1 = 0 \Leftrightarrow \left( {z + 1} \right)\left( {{z^2} - z + 1} \right) = 0\)

Nghiệm của \(z + 1 = 0\) là \({z_1} =  - 1\)

\({z^2} - z + 1 = 0 \Leftrightarrow {\left( {z - {1 \over 2}} \right)^2} =  - {3 \over 4} = {\left( {{{\sqrt 3 } \over 2}i} \right)^2}\)              

                      \( \Leftrightarrow \left[ \matrix{  z = {1 \over 2} + {{\sqrt 3 } \over 2}i = {z_2} \hfill \cr  z = {1 \over 2} - {{\sqrt 3 } \over 2}i = {z_3} \hfill \cr}  \right.\)

Vậy \(S = \left\{ { - 1;{1 \over 2} + {{\sqrt 3 } \over 2}i;{1 \over 2} - {{\sqrt 3 } \over 2}i} \right\}\)

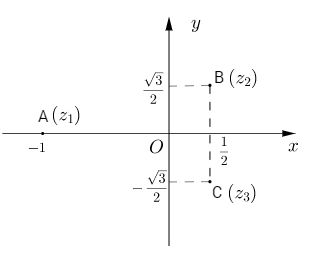
b) \({z^4} - 1 = 0 \Leftrightarrow \left( {{z^2} - 1} \right)\left( {{z^2} + 1} \right) = 0\)

                   \( \Leftrightarrow \left[ \matrix{  {z^2} - 1 = 0 \hfill \cr  {z^2} + 1 = 0 \hfill \cr}  \right. \Leftrightarrow \left[ \matrix{  z =  \pm 1 \hfill \cr  z =  \pm i \hfill \cr}  \right.\)

Phương trình có 4 nghiệm \({z_1} = i,{z_2} =  - i,{z_3} = 1,{z_4} =  - 1\)

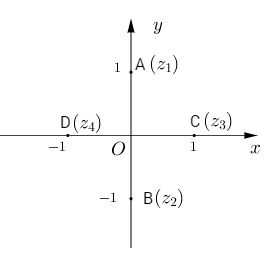
c) \({z^4} + 4 = 0 \Leftrightarrow \left( {{z^2} + 2i} \right)\left( {{z^2} - 2i} \right) = 0\)

Nghiệm của \({z^2} + 2i = 0\) là các căn bậc hai của -2i, đó là \({z_1} = 1 - i\),\({z_2} =  - 1 + i\)

Nghiệm của \({z^2} - 2i = 0\) là các căn bậc hai của 2i, đó là \({z_3} = 1 + i\),\({z_4} =  - 1 - i\)

Vậy \({z^4} + 4 = 0\) có bốn nghiệm \({z_1},{z_2},{z_3},{z_4}\).

d) \(8{z^4} + 8{z^3} = z + 1 \Leftrightarrow \left( {z + 1} \right)\left( {8{z^3} - 1} \right) = 0\)

                          \( \Leftrightarrow \left( {z + 1} \right)\left( {2z - 1} \right)\left( {4{z^2} + 2z + 1} \right) = 0\)

Nghiệm của \(z + 1 = 0\) là \({z_1} =  - 1\)

Nghiệm của \(2z - 1 = 0\) là \({z_2} = {1 \over 2}\)

Nghiệm của \(4{z^2} + 2z + 1 = 0\) hay \({\left( {2z + {1 \over 2}} \right)^2} + {3 \over 4} = 0\)là \({z_3} =  - {1 \over 4} + {{\sqrt 3 } \over 4}i\)  và\({z_4} =  - {1 \over 4} - {{\sqrt 3 } \over 4}i\)

Vậy phương trình đã cho có bốn nghiệm\({z_1},{z_2},{z_3},{z_4}\)

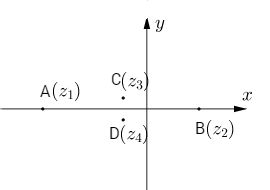
Bài 25 trang 199 SGK Đại số và Giải tích 12 Nâng cao

a) Tìm các số thực b, c để phương trình (với ẩn z):

                \({z^2} + bz + c = 0\) 

nhận \(z = 1 + i\) làm một nghiệm.

b) Tìm các số thực a, b, c để phương trình (với ẩn z):

                      \({z^3} + a{z^2} + bz + c = 0\) 

nhận \(z = 1 + i\) làm nghiệm và cũng nhận \(z = 2\) là nghiệm.

Giải

a) \(1 + i\) là một nghiệm của phương trình \({z^2} + bz + c = 0\) khi và chỉ khi

\({\left( {1 + i} \right)^2} + b\left( {1 + i} \right) + c = 0 \Leftrightarrow 2i + b + bi + c = 0\)

\( \Leftrightarrow b + c + \left( {2 + b} \right)i = 0\)

\(\Leftrightarrow \left\{ \matrix{  b + c = 0 \hfill \cr  2 + b = 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  b =  - 2 \hfill \cr  c = 2 \hfill \cr}  \right.\)

b) \(1 + i\) là một nghiệm của \({z^3} + a{z^2} + bz + c = 0\)  khi và chỉ khi

   \({\left( {1 + i} \right)^3} + a{\left( {1 + i} \right)^2} + b\left( {1 + i} \right) + c = 0 \)

\(\Leftrightarrow \left( {b + c - 2} \right)+\left( {2 + 2a + b} \right)i = 0\)

\( \Leftrightarrow \left\{ \matrix{  b + c - 2 = 0\,\,\,\,\,\,\,\,\left( 1 \right) \hfill \cr  2a + b + 2 = 0\,\,\,\,\,\left( 2 \right) \hfill \cr}  \right.\)

\(2\) là nghiệm của \({z^3} + a{z^2} + bz + c = 0\) khi và chỉ khi \(8 + 4a + 2b + c = 0\,\,\,\left( 3 \right)\)

Từ (1), (2), (3) ta có hệ: .\(\left\{ \matrix{  b + c = 2 \hfill \cr  2a + b =  - 2 \hfill \cr  4a + 2b + c =  - 8 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  a =  - 4 \hfill \cr  b = 6 \hfill \cr  c =  - 4 \hfill \cr}  \right.\) 

Bài 26 trang 199 SGK Đại số và Giải tích 12 Nâng cao

a) Dùng công thức cộng trong lượng giác để chứng minh rằng với mọi số thực \(\varphi \), ta có  \({\left( {\cos \varphi  + i\sin \varphi } \right)^2} = \cos 2\varphi  + i\sin 2\varphi \).

Từ đó hãy tìm mọi căn bậc hai của số phức \(\cos 2\varphi  + i\sin 2\varphi \). Hãy so sánh cách giải này với cách giải trong bài học ở bài 2.

b) Tìm các căn bậc hai của \({{\sqrt 2 } \over 2}\left( {1 - i} \right)\) bằng hai cách nói ở câu a).

Giải

a) Với mọi \(\varphi \) ta có: \({\left( {\cos \varphi  + i\sin \varphi } \right)^2} = {\cos ^2}\varphi  - {\sin ^2}\varphi  + \left( {2\sin \varphi \cos \varphi } \right)i\)

\( = \cos 2\varphi  + i\sin 2\varphi \)

Vậy các căn bậc hai của \(\cos 2\varphi  + i\sin 2\varphi \) là \( \pm \left( {\cos \varphi  + i\sin \varphi } \right)\)

Theo cách giải trong bài học, để tìm căn bậc hai của\(\cos 2\varphi  + i\sin 2\varphi \) ta giải hệ phương trình\(\left\{ \matrix{  {x^2} - {y^2} = \cos 2\varphi  \hfill \cr 2xy = \sin 2\varphi  \hfill \cr}  \right.\)

Rõ ràng hệ có các nghiệm \(\left( {\cos \varphi ,\sin \varphi } \right),\left( { - \cos \varphi , - \sin \varphi } \right)\) do đó\( \pm \left( {\cos \varphi  + i\sin \varphi } \right)\) là hai căn bậc hai của\(\cos 2\varphi  + i\sin 2\varphi \). Ta biết rằng chỉ có hai căn như thế nên đó là tất cả các căn bậc hai cần tìm.

b) \({{\sqrt 2 } \over 2}\left( {1 - i} \right) \)

\(= \cos {\pi  \over 4} - i\sin {\pi  \over 4} = \cos \left( { - {\pi  \over 4}} \right) + i\sin \left( { - {\pi  \over 4}} \right)\)

\(\text{ thì theo câu a) }, {{\sqrt 2 } \over 2}\left( {1 - i} \right)\) có hai căn bậc hai là \( \pm \left( {\cos \left( {{{ - \pi } \over 8}} \right) + i\sin \left( {{{ - \pi } \over 8}} \right)} \right) =  \pm \left( {\cos {\pi  \over 8} - i\sin {\pi  \over 8}} \right)\)

Mà \(\eqalign{  & \cos {\pi  \over 8} = \sqrt {{{1 + \cos {\pi  \over 4}} \over 2}}  = \sqrt {{{1 + {{\sqrt 2 } \over 2}} \over 2}} \cr& = {1 \over 2}\sqrt {2 + \sqrt 2 }   \cr  & \sin {\pi  \over 8} = \sqrt {{{1 - \cos {\pi  \over 4}} \over 2}}  = \sqrt {{{1 - {{\sqrt 2 } \over 2}} \over 2}} \cr& = {1 \over 2}\sqrt {2 - \sqrt 2 }  \cr} \)

Vậy hai căn bậc hai cần tìm là \( \pm {1 \over 2}\left( {\sqrt {2 + \sqrt 2 }  - i\sqrt {2 - \sqrt 2 } } \right)\)

Còn theo bài học, việc tìm các căn bậc hai của\({{\sqrt 2 } \over 2}\left( {1 - i} \right)\) đưa về việc giải hệ phương trình\(\left\{ \matrix{  {x^2} - {y^2} = {{\sqrt 2 } \over 2} \hfill \cr  2xy =  - {{\sqrt 2 } \over 2} \hfill \cr}  \right.\)

Hệ đó tương đương với \(\left\{ \matrix{  8{x^4} - 4\sqrt 2 {x^2} - 1 = 0 \hfill \cr  y =  - {{\sqrt 2 } \over {4x}} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x^2} = {{\sqrt 2  + 2} \over 4} \hfill \cr  y =  - {{\sqrt 2 } \over {4x}} \hfill \cr}  \right.\)

nên có các nghiệm là: \(\left( {{{\sqrt {2 + \sqrt 2 } } \over 2};{{ - \sqrt {2 - \sqrt 2 } } \over 2}} \right),\left( {{{ - \sqrt {2 + \sqrt 2 } } \over 2};{{\sqrt {2 - \sqrt 2 } } \over 2}} \right)\)

Vậy ta lại được hai căn bậc hai đã viết ở trên.  

Giaibaitap.me