Bài 14 trang 17 SGK Đại số và Giải tích 12 Nâng cao
Xác định các hệ số \(a,b, c\) sao cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) đạt cực trị bằng \(0\) tại điểm \(x=-2\) và đồ thị của hàm số đi qua điểm \(A\left( {1;0} \right)\).
Giải
\(f'\left( x \right) = 3{x^2} + 2ax + b\)
\(f\) đạt cực trị tại điểm \(x=-2\) nên \(f'\left( { - 2} \right) = 0\)
\( \Rightarrow \)\(\,12 - 4a + b = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
\(f\left( { - 2} \right) = 0 \Rightarrow - 8 + 4a - 2b + c = 0\,\,\,\,\left( 2 \right)\)
Đồ thị hàm số đi qua điểm \(A\left( {1;0} \right)\) nên: \(f\left( 1 \right) = 0 \Rightarrow 1 + a + b + c = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\)
Từ (1), (2), (3) ta có hệ phương trình:
\(\left\{ \matrix{
4a - b = 12 \hfill \cr
4a - 2b + c = 8 \hfill \cr
a + b + c = - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 3 \hfill \cr
b = 0 \hfill \cr
c = - 4 \hfill \cr} \right.\)
Vậy \(a=3, b=0, c=-4\).
Bài 15 trang 17 SGK Đại số và Giải tích 12 Nâng cao
Chứng minh rằng với mọi giá trị của \(m\), hàm số: \(y = {{{x^2} - m\left( {m + 1} \right)x + {m^3} + 1} \over {x - m}}\) luôn có cực đại và cực tiểu
Giải
TXĐ: \(D = {\mathbb{R}}\backslash \left\{ m \right\}\)
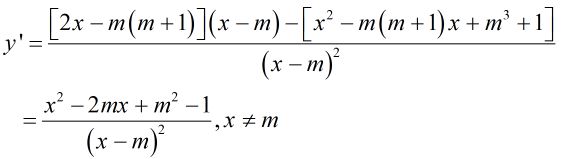
\(\eqalign{
& \;\;\;\;\;y' = 0\cr& \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0 \Leftrightarrow {\left( {x - m} \right)^2} = 1 \cr
& \Leftrightarrow \left[ \matrix{
x = m - 1;f\left( {m - 1} \right) = - {m^2} + m - 2 \hfill \cr
x = m + 1;f\left( {m + 1} \right) = - {m^2} + m + 2 \hfill \cr} \right. \cr} \)
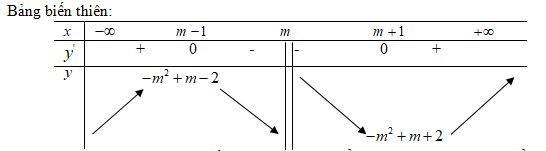
Với mọi giá trị của \(m\), hàm số đạt cực đại tại điểm \(x=m-1\) và đạt cực tiểu tại điểm \(x=m+1\)
Giaibaitap.me
Giải bài tập trang 22 bài 3 giá trị lớn nhất và giá trị nhỏ nhất của hàm số SGK Giải tích 12 Nâng cao. Câu 16: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số...
Giải bài tập trang 22, 23 bài 3 giá trị lớn nhất và giá trị nhỏ nhất của hàm số SGK Giải tích 12 Nâng cao. Câu 19: Cho một tam giác đều ABC cạnh a...
Giải bài tập trang 22, 23, 24 bài 3 giá trị lớn nhất và giá trị nhỏ nhất của hàm số SGK Giải tích 12 Nâng cao. Câu 23: Độ giảm huyết áp của một bệnh nhân được cho bởi công thức...
Giải bài tập trang 22, 23, 24 bài 3 giá trị lớn nhất và giá trị nhỏ nhất của hàm số SGK Giải tích 12 Nâng cao. Câu 26: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số ...
