Bài 19 trang 22 SGK Đại số và Giải tích 12 Nâng cao

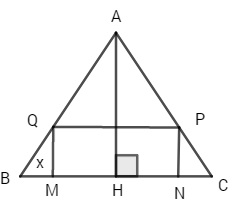
Cho một tam giác đều \(ABC\) cạnh \(a\). Người ta dựng một hình chữ nhật \(MNPQ\) có cạnh \(MN\) nằm trên cạnh \(BC\), hai đỉnh \(P\) và \(Q\) theo thứ tự nằm trên hai cạnh \(AC\) và \(AB\) của tam giác. Xác định vị trí của điểm \(M\) sao cho hình chữ nhật có diện tích lớn nhất và tìm giá trị lớn nhất đó.

Giải

Đặt \(BM = x\left( {0 < x < {a \over 2}} \right)\)

Gọi \(H\) là trung điểm \(BC\) ta có \(AH = {{a\sqrt 3 } \over 2}\)

\(\Delta BMQ = \Delta CNP\,\,\, \Rightarrow BM = NC = x\)

\(\Rightarrow MN = a - 2x\)

\(QM//AH\) nên \({{QM} \over {AH}} = {{BM} \over {BH}} \Rightarrow QM = {{AH.BM} \over {BH}} = {{{{a\sqrt 3 } \over 2}.x} \over {{a \over 2}}} = x\sqrt 3 \)

Diện tích hình chữ nhật \(MNPQ\) là

\(S\left( x \right) = MN.QM \)

           \(= \left( {a - 2x} \right).x\sqrt 3  = \sqrt 3 \left( {ax - 2{x^2}} \right)\)

Ta tìm giá trị lớn nhất của \(S\left( x \right)\) trên khoảng \(\left( {0;{a \over 2}} \right)\)

Ta có : \(S'\left( x \right) = \sqrt 3 \left( {a - 4x} \right);\)

\(S'\left( x \right) = 0 \Leftrightarrow x = {a \over 4};S\left( {{a \over 4}} \right) = {{\sqrt 3 } \over 8}{a^2}\)

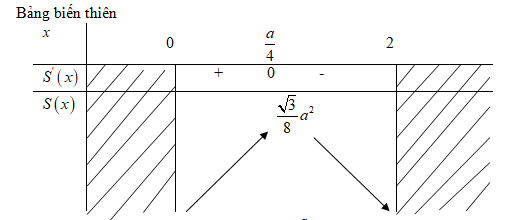
      Vậy \(S\left( x \right)\) đạt giá trị lớn nhất tại điểm \(x = {a \over 4}\) và giá trị lớn nhất của diện tích hình chữ nhật là: \(\mathop {\max \,\,\,S\left( x \right)}\limits_{x \in \left( {0;{a \over 2}} \right)}  = S\left( {{a \over 4}} \right) = {{\sqrt 3 } \over 8}{a^2}\)

Bài 20 trang 22, SGK Đại số và Giải tích 12 Nâng cao

Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá thì trung bình mỗi con cá sau một vụ cân nặng: \(P(n)=480 – 20n^2\).

Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.

Giải

Nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá thì sau một vụ, số cá trên mỗi đơn vị diện tích mặt hồ trung bình cân nặng:

Xét hàm số \(f\left( x \right) = 480 - 20{x^2}\) trên khoảng \(\left( {0; + \infty } \right)\)

( Biến số \(n \in {\mathbb{N}}^*\) được thay bằng biến số \(x \in \left( {0; + \infty } \right)\))

Ta có \(f'\left( x \right) = 480 - 40x;f'\left( x \right) = 0 \Leftrightarrow x = 12\)

Bảng biến thiên:

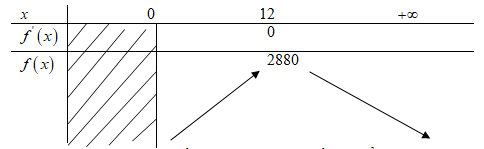
Trên khoảng \(\left( {0; + \infty } \right)\), hàm số \(f\) đạt giá trị lớn nhất tại điểm \(x=12\). Từ đó suy ra rằng trên tập \(\mathbb N^*\) các số nguyên dương, hàm số \(f\) đạt giá trị lớn nhất tại điểm \(n=12\).

Vậy muốn thu hoạch được nhều nhất sau một vụ thì trên mỗi đơn vị diện tích của mặt hồ phải thả \(12\) con cá.

Bài 21 trang 22 SGK Đại số và Giải tích 12 Nâng cao

Tìm cực trị của các hàm số sau:

a) \(f\left( x \right) = {x \over {{x^2} + 1}};\)                    b) \(f\left( x \right) = {{{x^3}} \over {x + 1}};\)

c) \(f\left( x \right) = \sqrt {5 - {x^2}} ;\)              d) \(f\left( x \right) = x + \sqrt {{x^2} - 1} \).

Giải

a) TXĐ: \(D = {\mathbb{R}}\)

\(f'\left( x \right) = {{{x^2} + 1 - 2{x^2}} \over {{{\left( {{x^2} + 1} \right)}^2}}} = {{1 - {x^2}} \over {{{\left( {{x^2} + 1} \right)}^2}}};f'\left( x \right) = 0\)

\(\Leftrightarrow \left[ \matrix{
x = 1\,\,\,\,\,\,f\left( 1 \right) = {1 \over 2} \hfill \cr 
x = - 1\,\,\,f\left( { - 1} \right) = - {1 \over 2} \hfill \cr} \right.\)

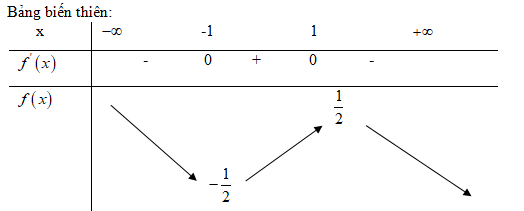
Hàm số đạt cực tiểu tại điểm \(x=-1\), giá trị cực tiểu \(f\left( { - 1} \right) =  - {1 \over 2}\). Hàm số đạt cực đại tại điểm \(x=1\), giá trị cực đại \(f\left( 1 \right) = {1 \over 2}\).

b) TXĐ: \(D = {\mathbb {R}}\backslash \left\{ { - 1} \right\}\)

\(\eqalign{
& f'\left( x \right) = {{3{x^2}\left( {x + 1} \right) - {x^3}} \over {{{\left( {x + 1} \right)}^2}}} = {{2{x^3} + 3{x^2}} \over {{{\left( {x + 1} \right)}^2}}} \cr 
& f'\left( x \right) = 0 \Leftrightarrow {x^2}\left( {2x + 3} \right) = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr 
x = - {3 \over 2} \hfill \cr} \right. \cr 
& f\left( { - {3 \over 2}} \right) = {{27} \over 4} \cr} \)

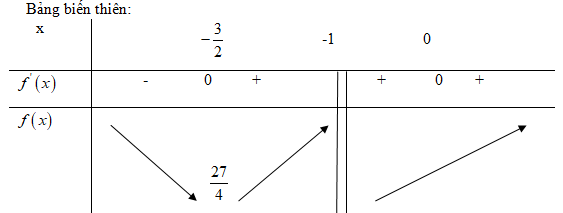
Hàm số đạt cực tiểu tại điểm \(x =  - {3 \over 2}\), giá trị cực tiểu \(f\left( { - {3 \over 2}} \right) = {{27} \over 4}\).

c) TXĐ: \(D = \left[ { - \sqrt 5 ;\sqrt 5 } \right]\)

\(f'\left( x \right) = {{ - 2x} \over {2\sqrt {5 - {x^2}} }} = {{ - x} \over {\sqrt {5 - {x^2}} }};f'\left( x \right) = 0 \)

\(\Leftrightarrow x = 0;f\left( 0 \right) = \sqrt 5 \)

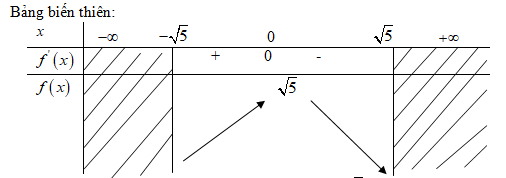
Hàm số đạt cực đại tại \(x=0\), giá trị cực đại \(f\left( 0 \right) = \sqrt 5 \).

d) \(f\left( x \right)\) xác định khi và chỉ khi \({x^2} - 1 \ge 0\) \( \Leftrightarrow x \le  - 1\)hoặc \(x \ge 1\).

TXĐ: \(D = \left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)\)

\(f'\left( x \right) = 1 + {x \over {\sqrt {{x^2} - 1} }} = {{\sqrt {{x^2} - 1}  + x} \over {\sqrt {{x^2} - 1} }}\) 

\(f'\left( x \right) = 0 \Leftrightarrow \sqrt {{x^2} - 1} = - x \Leftrightarrow \left\{ \matrix{
x \le 0 \hfill \cr 
{x^2} - 1 = {x^2} \hfill \cr} \right.\) vô nghiệm

\(f'\left( { - 2} \right) < 0 \Rightarrow f'\left( x \right) < 0\) với mọi \(x <  - 1\)

\(f'\left( { - 2} \right) > 0 \Rightarrow f'\left( x \right) > 2\) với mọi \(x > 1\)

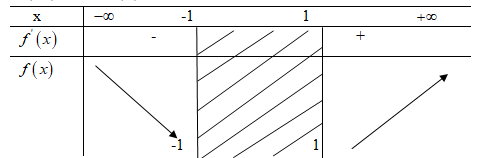
Hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right]\) và đồng biến trên \(\left[ {1; + \infty } \right)\).

Hàm số không có cực trị.

Bài 22 trang 23 SGK Đại số và Giải tích 12 Nâng cao

Tìm giá trị của \(m\) để hàm số \(f\left( x \right) = {{{x^2} + mx - 1} \over {x - 1}}\) có cực đại và cực tiểu.

Giải

TXĐ: \(D = {\mathbb{R}}\backslash \left\{ 1 \right\}\)

\(f'\left( x \right) = {{\left( {2x + m} \right)\left( {x - 1} \right) - \left( {{x^2} + mx - 1} \right)} \over {{{\left( {x - 1} \right)}^2}}} = {{{x^2} - 2x + 1 - m} \over {{{\left( {x - 1} \right)}^2}}}\)

\(f'\left( x \right) = 0 \Leftrightarrow {x^2} - 2x + 1 - m = 0\) (1)

Hàm số \(f\) có cực đại và cực tiểu khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác \(1\), tức là

\(\left\{ \matrix{
\Delta ' = m > 0 \hfill \cr 
{1^2} - 2.1 + 1 - m \ne 0 \hfill \cr} \right. \Leftrightarrow m > 0\) .

Vậy \(m>0\) thì hàm số \(f\left( x \right)\) có cực đại và cực tiểu.

Giaibaitap.me