Bài 1 trang 7 SGK Đại số và Giải tích 12 Nâng cao

Xét chiều biến thiên của các hàm số sau:

a) \(y = 2{x^3} + 3{x^2} + 1\)        b) \(y = {x^3} - 2{x^2} + x + 1\)

c) \(y = x + {3 \over x}\)                      d) \(y = x - {2 \over x}\)

e) \(y = {x^4} - 2{x^2} - 5\)          f) \(y = \sqrt {4 - {x^2}} \)

Giải

a) Tập xác định: \(D =\mathbb R\)

\(\eqalign{
& y' = 6{x^2} + 6x \cr 
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 0\,\,\left( {y = 1} \right) \hfill \cr 
x = - 1\,\,\left( {y = 2} \right) \hfill \cr} \right. \cr} \)

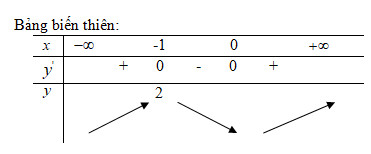
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0; + \infty } \right)\) nghịch biến trên khoảng \(\left( { - 1;0} \right)\).

b) Tập xác định: \(D =\mathbb R\)

\(\eqalign{
& y' = 3{x^2} - 4x + 1 \cr 
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 1\,\,\left( {y = 1} \right) \hfill \cr 
x = {1 \over 3}\,\,\left( {y = {{31} \over {27}}} \right) \hfill \cr} \right. \cr} \)

Bảng biến thiên

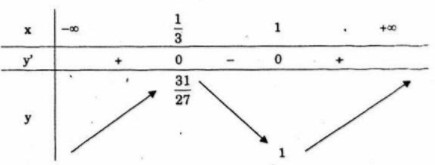
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;{1 \over 3}} \right)\) và \(\,\left( {1; + \infty } \right)\) , nghịch biến trên khoảng \(\,\left( {{1 \over 3};1} \right)\).

c) Tập xác định: \(D =\mathbb R\backslash \left\{ 0 \right\}\)

\(\eqalign{
& y' = 1 - {3 \over {{x^2}}} = {{{x^2} - 3} \over {{x^2}}} \cr 
& y' = 0 \Leftrightarrow \left[ \matrix{
x = \sqrt 3 \,\,\left( {y = 2\sqrt 3 } \right) \hfill \cr 
x = - \sqrt 3 \,\,\left( {y = - 2\sqrt 3 } \right) \hfill \cr} \right. \cr} \)

Bảng biến thiên

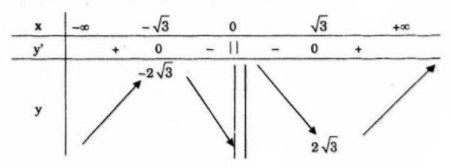
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - \sqrt 3 } \right)\) và \(\,\left( {\sqrt 3 ; + \infty } \right)\) , nghịch biến trên khoảng \(\left( { - \sqrt 3 ;0} \right)\) và \(\,\left( {0;\sqrt 3 } \right)\).

d) Tập xác định: \(D = \mathbb R\backslash \left\{ 0 \right\}\)

\(y' = 1 + {2 \over {{x^2}}} > 0\) với mọi \(x \ne 0\)

Hàm số đồng biến trên mỗi khoảng \(\,\,\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).

e) Tập xác định: \(D= \mathbb R\)

\(y' = 4{x^3} - 4x = 4x\left( {{x^2} - 1} \right);y' = 0 \)

\( \Leftrightarrow \,\left[ \matrix{
x = 0\,\,\,\,\left( {y = - 5} \right) \hfill \cr 
x = \pm 1\,\,\,\,\left( {y = - 6} \right) \hfill \cr} \right.\)

Bảng biến thiên

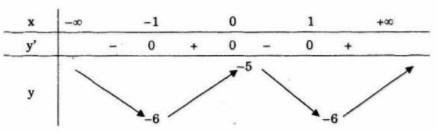
Hàm số đồng biến trên mỗi khoảng \(\,\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\), đồng biến trên mỗi khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).

f) Hàm số xác định khi và chỉ khi \(4 - {x^2} \ge 0 \Leftrightarrow  - 2 \le x \le 2\)

Tập xác định: \(D = \left[ { - 2;2} \right]\)

\(y' = {{ - 2x} \over {2\sqrt {4 - {x^2}} }} = {{ - x} \over {\sqrt {4 - {x^2}} }};y' = 0 \Leftrightarrow \)\(x = 0\,\,\,\left( {y = 2} \right)\)

Bảng biến thiên

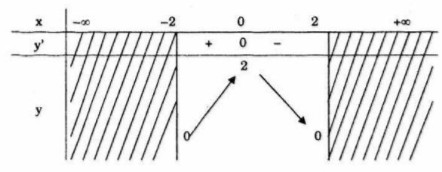
Hàm số đồng biến trên khoảng \(\left( { - 2;0} \right)\) và nghịch biến trên khoảng \(\left( {0;2} \right)\) .

Bài 2 trang 7 SGK Đại số và Giải tích 12 Nâng cao

Chứng minh rằng:

a) Hàm số \(y = {{x - 2} \over {x + 2}}\) đồng biến trên mỗi khoảng xác định của nó;

b)Hàm số \(y = {{ - {x^2} - 2x + 3} \over {x + 1}}\) nghịch biến trên mỗi khoảng xác định của nó.

Giải

a) Tập xác định \(D =\mathbb R\backslash \left\{ { - 2} \right\}\)

\(y' = {{\left| \matrix{
1\,\,\,\, - 2 \hfill \cr 
1\,\,\,\,\,\,\,\,2 \hfill \cr} \right|} \over {{{\left( {x + 2} \right)}^2}}} = {4 \over {{{\left( {x + 2} \right)}^2}}} > 0\) với mọi \(x \ne  - 2\)

Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).

b) Tập xác định \(D =\mathbb R\backslash \left\{ { - 1} \right\}\)

\(y' = {{\left( { - 2x - 2} \right)\left( {x + 1} \right) - \left( { - {x^2} - 2x + 3} \right)} \over {{{\left( {x + 1} \right)}^2}}} = {{ - {x^2} - 2x - 5} \over {{{\left( {x + 1} \right)}^2}}} < 0\) với mọi \(x \ne  - 1\).

Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).

Bài 3 trang 8 SGK Đại số và Giải tích 12 Nâng cao

Chứng minh rằng các hàm số sau đây đồng biến trên \(\mathbb R\):

a) \(f\left( x \right) = {x^3} - 6{x^2} + 17x + 4;\) 

b) \(f\left( x \right) = {x^3} + x - \cos x - 4\)

Giải

a) Tập xác định: \(D =\mathbb R\)

\(f'\left( x \right) = 3{x^2} - 12x + 17 > 0\) với mọi \(x \in \mathbb R\) (vì \(a > 0,\Delta ' < 0\))

Hàm số đồng biến trên \(\mathbb R\).

b) Tập xác định: \(D =\mathbb R\)

\(f'\left( x \right) = 3{x^2} + 1 + \sin x\)

Vì \(1 + \sin x \ge 0\) và \(3{x^2} \ge 0\) nên \(f'\left( x \right) \ge 0\) với mọi \(x \in \mathbb R\), với \(x = 0\) thì \(1 + \sin x = 1 > 0\) nên \(f'\left( x \right) > 0\,\,\,\forall x \in \mathbb R\) do đó hàm số đồng biến trên \(\mathbb R\).

Giaibaitap.me