Bài 1 trang 30 SGK Hình học 12 Nâng cao

Cho tứ diện \(ABCD\) có thể tích bằng \(V\). Gọi \(B'\) và \(D'\) lần lượt là trung điểm của \(AB\) và \(AD\). Mặt phắng \((CB'D')\) chia khối tứ diện thành hai phần. Tính thể tích mỗi phần đó.

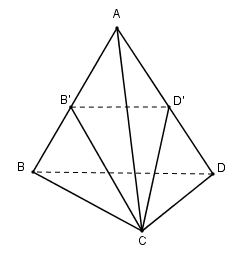
Mp \((CB’D’)\) chia khối tứ diện thành hai khối chóp \(C.AB’D’\) và \(C.BB’D’D\). Hai khối chóp này có chiều cao bằng nhau.
Mặt khác: \({S_{AB'D'}} = {1 \over 4}{S_{ABD}} \Rightarrow {V_{C.AB'D'}} = {1 \over 4}V\)
Do đó \({V_{C.BB'D'D}} = {3 \over 4}V\)

Bài 2 trang 31 SGK Hình học 12 Nâng cao

Cho khối hộp \(ABCD.A'B'C'D'\). Chứng minh rằng sáu trung điểm của sáu cạnh \(AB, BC, CC', C'D’, D'A'\) và \(A'A\) nằm trên một mặt phẳng và mặt phẳng đó chia khối hộp thành hai phần có thể tích bằng nhau.

Giải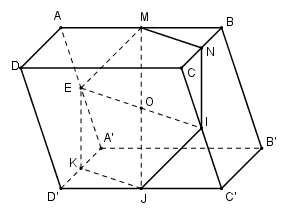

Gọi \(M, N, I, J, K, E\) lần lượt là trung điểm của các cạnh \(AB, BC, CC’, C’D’, D’A’, A’A\) của khối hộp \(ABCD.A’B’C’D’\) tâm \(O\).
Ta có \(O\) là tâm hình bình hành \(ABC’D’\) nên \(M, O, J\) thẳng hàng (\(O\) là trung điểm của \(MJ\)). Mặt khác ba đường thẳng \(MN, EI\) và \(KJ\) đôi một song song với nhau (vì cung song song với \(AC\)) nên chúng đồng phẳng.
Vậy \(6\) điểm \(M, N, I, J, K, E\) cùng nằm trên một mặt phẳng \(\left( \alpha  \right)\).
Mp \(\left( \alpha  \right)\) chia khối hộp thành hai khối đa diện khối thứ nhất có các đỉnh \(M, N, I, J, K, E, A, C, D, D’\) , khối thứ hai có các đỉnh \(M, N, I, J, K, E, C’, A’, B, B’\).
Phép đối xứng qua điểm \(O\) biến tập hợp đỉnh của khối đa diện thứ nhất thành tập hợp đỉnh của khối đa diện thứ hai. Suy ra hai khối đa diện đó bằng nhau và do đó có thể tích bằng nhau.

Bài 3 trang 31 SKG Hình học 12 Nâng cao

Cho khối tứ diện \(ABCD, E\) và \(F\) lần lượt là trung điểm của hai cạnh \(AB\) và \(CD\). Hai mặt phẳng \((ABF)\) và \((CDE)\) chia khối tứ diện \(ABCD\) thành bốn khối tứ diện.

a) Kể tên bốn khối tứ diện đó.

b) Chứng tỏ rằng bốn khôi tứ diện đó có thể tích bằng nhau.

c) Chứng tỏ rằng nếu \(ABCD\) là khối tứ diện đều thì bốn khối tứ diện nói trên bằng nhau.

Giải

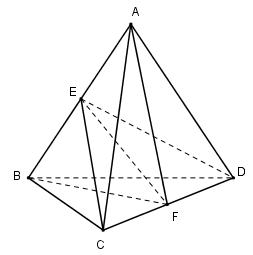
a) Hai mặt phẳng \((ABF)\) và \((CDE)\) chia khối tứ diện \(ABCD\) thành bốn khối tứ diện \(ADEF, ACEF, BDEF, BCEF\)

b) Vì \(F\) là trung điểm của \(CD\) nên mp \((ABF)\) chia khối tứ diện \(ABCD\) thành hai khối tứ diện \(ABCF\) và \(ABDF\) có thể tích bằng nhau.

Vì \(E\) là trung điểm của \(AB\) nên mp \((CDE)\) lại chia mỗi khối tứ diện \(ABCF\) và \(ABDF\) thành hai khối tứ diện có thể tích bằng nhau.

Vậy \({V_{ADEF}} = {V_{ACEF}} = {V_{BDEF}} = {V_{BCEF}}\)

c) Nếu \(ABCD\) là tứ diện đều thì nó nhận mp \((ABF)\) và mp \((CDE)\) làm các mặt phẳng đối xứng và phép đối xứng qua đường thẳng \(EF\) biến tứ diện \(ADEF\) thành tứ diện \(BCEF\). Từ đó suy ra:

Khối tứ diện \(ADEF\) bằng khối tứ diện \(ACEF\) (vì chúng đối xứng với nhau qua mp \((ABF)\))

Khối tứ diện \(ADEF\) bằng khối tứ diện \(BDEF\) (vì chúng đối xứng với nhau qua mp \((CDE)\))

Khối tứ diện \(ADEF\) bằng khối tứ diện \(BCEF\) (vì phép đối xứng qua trục \(EF\) biến tứ diện này thành tứ diện kia)

Giaibaitap.me