Bài 1 trang 45 SGK Hình học 12 Nâng cao

Trong không gian cho ba đoạn thẳng \(AB, BC, CD\) sao cho \(AB \bot BC\,\,,\,\,BC \bot CD\,\,,\,\,CD \bot AB\) . Chứng minh rằng có mặt cầu đi qua bốn điểm \(A, B, C, D\). Tính bán kính mặt cầu đó nếu \(AB = a\,\,,\,\,BC = b\,\,,\,\,CD = c\) .

Giải

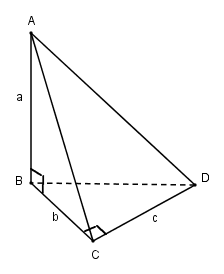
Vì \(AB \bot BC\) và \(AB \bot CD\) nên \(AB \bot \left( {BCD} \right)\). Suy ra \(AB \bot BD\)

Vì \(CD \bot BC\) và \(CD \bot AB\) nên \(CD \bot \left( {ABC} \right) \Rightarrow CD \bot AC\)

Gọi \(I\) là trung điểm \(AD\), ta có \(IB = IA = ID = IC\) nên các điểm \(A, B, C, D\) cùng nằm trên mặt cầu đường kính \(AD\).

Mặt khác ta có: \(A{D^2} = A{B^2} + B{D^2} = A{B^2} + B{C^2} + C{D^2} \)

\(= {a^2} + {b^2} + {c^2}\)

Do đó bán kính mặt cầu là \(R = {1 \over 2}AD = {1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)

Bài 2 trang 45 SGK Hình học 12 Nâng cao

a) Tìm tập hợp tâm các mặt cầu đi qua hai điểm phân biệt \(A, B\) cho trước.

b) Tìm tập hợp tâm các mặt cầu đi qua hai điểm phân biệt \(A, B, C\) cho trước.

c) Tìm tập hợp tâm các mặt cầu đi qua một đường tròn cho trước.

d) Có hay không một mặt cầu đi qua một đường tròn và một điểm nằm ngoài mặt phẳng chứa đường tròn.

Giải

a) \(I\) là tâm của các mặt cầu đi qua hai điểm phân biệt \(A, B\) cho trước khi và chỉ khi \(IA = IB\). Vậy tập hợp tâm của các mặt cầu đó là mặt phẳng trung trực của đoạn thẳng \(AB\).

b) \(I\) là tâm của mặt cầu đi qua ba điểm phân biệt \(A, B, C\) cho trước khi và chỉ khi \(IA = IB = IC\). Vậy:

+ Nếu ba điểm \(A, B, C\) không thẳng hàng thì tập hợp các điểm \(I\) là trục của đường trong ngoại tiếp tam giác \(ABC\).

+ Nếu ba điểm \(A, B, C\) thẳng hàng thì tập hợp các điểm \(I\) là rỗng.

c) \(I\) là tâm của mặt cầu đi qua đường tròn \((C)\) cho trước khi và chỉ khi \(I\) cách đều mọi điểm của đường tròn. Vậy tập hợp các điểm \(I\) là trục của đường tròn \((C)\).

d) Gọi \(M\) là một điểm nằm ngoài mặt phẳng chứa đường tròn \((C)\). Lấy điểm \(A\) nằm trên \((C)\) và gọi \(I\) là giao điểm của trục đường tròn và mặt phẳng trung trực của \(MA\). Khi đó mặt cầu tâm \(I\), bán kính \(R = IA = IM\) là mặt cầu đi qua đường tròn \((C)\) và đi qua điểm \(M\).

Bài 3 trang 45 SGK Hình học 12 Nâng cao

Cho điểm \(M\) nằm trong mặt cầu \((S)\). Trong các mệnh đề sau đây, mệnh đề nào đúng?

a) Mọi mặt phẳng đi qua điểm \(M\) đều cắt \((S)\) theo một đường tròn.

b) Mọi đường thẳng đi qua \(M\) đều cắt \((S)\) tại hai điểm phân biệt.

Giải

Cả a) và b) đều đúng.

Bài 4 trang 45 SGK Hình học 12 Nâng cao

Cho đường thẳng \(d\) và điểm \(A\) không nằm trên \(d\). Xét các mặt cầu đi qua \(A\) và có tâm nằm trên \(d\). Chứng minh rằng các mặt cầu đó luôn đi qua một đường tròn cố định.

Giải

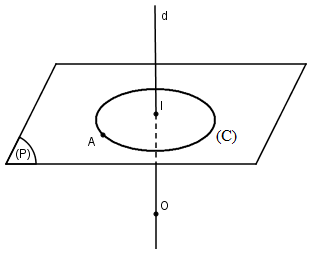
Giả sử \((S)\) là một mặt cầu đi qua \(A\) và có tâm \(O\) nằm trên \(d\). Gọi \((P)\) là mặt phẳng đi qua \(A\) và vuông góc với \(d\), \((P)\) cắt mặt cầu \((S)\) theo đường tròn \((C)\) có tâm là giao điểm \(I\) của \((P)\) và \(d\), có bán kính \(r = IA\). Vậy đường tròn \((C)\) cố định và mặt cầu \((S)\) luôn luôn đi qua \((C)\).

Giaibaitap.me