Bài 4 trang 31 SGK Hình học 12 Nâng cao

Cho khối làng trụ đứng \(ABC.A’B'C’\) có diện tích đáy bằng \(S\) và \(AA' = h\). Một mặt phẳng \((P)\) cắt các cạnh \(AA', BB’, CC'\) lần lượt tại \({A_1},{B_1}\) và . Biết \(A{A_1} = a,B{B_1} = b,CC' = c\).

a) Tính thể tích hai phần của khối lăng trụ được phân chia bởi mặt phẳng \((P)\).

b) Với điều kiện nào của \(a, b, c\) thì thể tích hai phần đó bằng nhau ?

Giải

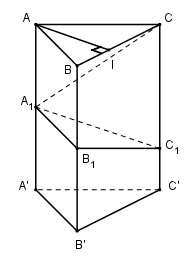
a) Kẻ đường cao \(AI\) của tam giác \(ABC\) thì \(AI \bot \left( {BCC'B'} \right)\) \(\Rightarrow AI = d\left( {{A_1};\left( {BCC'B'} \right)} \right)\). Ta có:

\(\eqalign{
& {V_{_{ABC.{A_1}{B_1}{C_1}}}} = {V_{{A_1}.ABC}} + {V_{{A_1}BC{C_1}{B_1}}} \cr
& = {1 \over 3}{\rm{aS + }}{1 \over 3}{S_{BC{C_1}{B_1}}}.AI \cr
& = {1 \over 3}aS + {1 \over 3}.{1 \over 2}\left( {b + c} \right).BC.AI \cr
& = {1 \over 3}aS + {1 \over 3}\left( {b + c} \right)S = {1 \over 3}\left( {a + b + c} \right)S \cr
& {V_{{A_1}{B_1}{C_1}A'B'C'}} = {V_{ABC.A'B'C'}} - {V_{ABC.{A_1}{B_1}{C_1}}} \cr
& = Sh - {1 \over 3}\left( {a + b + c} \right)S \cr&= {1 \over 3}\left[ {\left( {h - a} \right) + \left( {h - c} \right) + \left( {h - c} \right)} \right]S \cr} \)

b) \({V_{ABC.{A_1}{B_1}{C_1}}} = {V_{{A_1}{B_1}{C_1}.A'B'C'}} \)

\(\Leftrightarrow {1 \over 3}\left( {a + b + a} \right)S = {1 \over 2}Sh \Leftrightarrow 3h = 2\left( {a + b + c} \right)\)

Bài 5 trang 31 SKG Hình học 12 Nâng cao

Cho khối lăng trụ đểu \(ABC.A'B'C’\) và \(M\) là trung điểm của cạnh \(AB\). Mặt phẳng \((B'CM)\) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích hai phần đó.

Giải

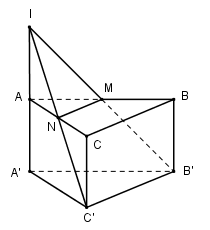
Gọi \(I\) là giao điểm của đường thẳng \(B’M\) với \(AA’\); \(N\) là giao điểm của \(IC’\) với \(AC\). Khi đó \(A\) là trung điểm của \(A’I\) và \(N\) là trung điểm của \(AC\).

Đặt \({S_{ABC}} = S\) và \(AA' = h\)

Thiết diện của mp \((B’C’M)\) với khối lăng trụ \(ABC.A’B’C’\) là hình thang cân \(MNC’B’\). Mp \((B’C’M)\) chia khối lăng trụ thành hai phần, phần chứa cạnh \(AA’\) có thể tích là \({V_1}\), phần còn lại có thể tích là \({V_2}\). Khi đó ta có:

\(\eqalign{
& {V_1} = {V_{AMN.A'B'C'}} = {V_{I.A'B'C'}} - {V_{I.AMN}}\cr& = {1 \over 3}S.2h - {1 \over 3}.{S \over 4}h \cr
& = {2 \over 3}Sh - {1 \over {12}}Sh = {7 \over {12}}Sh = {7 \over {12}}\left( {{V_1} + {V_2}} \right) \cr
& \Rightarrow 12{V_1} = 7{V_1} + 7{V_2} \Rightarrow {{{V_1}} \over {{V_2}}} = {7 \over 5} \cr} \)

Bài 6 trang 31 SGK Hình học 12 Nâng cao

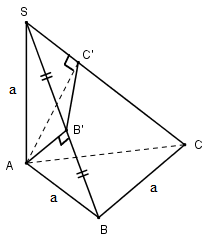
Cho khối chóp \(S.ABC\) có đường cao \(SA\) bằng \(a\), đáy là tam giác vuông cân có \(AB = BC = a\). Gọi \(B'\) là trung điểm của \(SB, C'\) là chân đường cao hạ từ \(A\) của tam giác \(SAC\).

a) Tính thể tích khối chóp \(S.ABC\).

b) Chứng minh rằng \(SC\) vuông góc với mp \((AB'C')\).

c) Tính thể tích khối chóp \(S.AB’C’\).

Giải

a) Thể tích khối chóp \(S.ABC\) là: \({V_{S.ABC}} = {1 \over 3}{S_{ABC}}.SA = {1 \over 6}{a^2}.a = {{{a^3}} \over 6}\)

b) Ta có \(BC \bot BA\) và \(BC \bot SA\) nên do đó \(AB' \bot BC\)

Ta có \(AB' \bot SB\) và \(AB' \bot BC\) nên \(AB' \bot SC\) (do \(AB' \bot \left( {SBC} \right)\) )

Theo giả thiết \(SC \bot AC'\), \(SC \bot AB'\) (chứng minh trên) \( \Rightarrow SC \bot \left( {AB'C'} \right)\)

c) Ta có \(AC’\) là đường cao trong tam giác vuông \(SAC\) nên \({{SC'} \over {SC}} = {{SC'.SC} \over {S{C^2}}} = {{S{A^2}} \over {S{C^2}}} = {{{a^2}} \over {3{a^2}}} = {1 \over 3}\)

Từ đó suy ra \({{{V_{S.AB'C'}}} \over {{V_{S.ABC}}}} = {{SA} \over {SA}}.{{SB'} \over {SB}}.{{SC'} \over {SC}} = {1 \over 2}.{1 \over 3} = {1 \over 6}\)

Vì \({V_{S.ABC}} = {{{a^3}} \over 6}\) nên \({V_{S.AB'C'}} = {{{a^3}} \over {36}}\)

Giaibaitap.me