Bài 5 trang 45 SGK Hình học 12 Nâng cao

Trong các mệnh đề sau đây, mệnh đề nào đúng?

a) Nếu hình đa diện nội tiếp mặt cầu thì mọi mặt của nó là đa giác nội tiếp đường tròn.

b) Nếu tất cả các mặt của một hình đa diện nội tiếp đường tròn thì đa diện đó nội tiếp mặt cầu.

Giải

a) Đúng vì mặt phẳng cắt mặt cầu theo một đường tròn.

b) Không đúng, chẳng hạn:

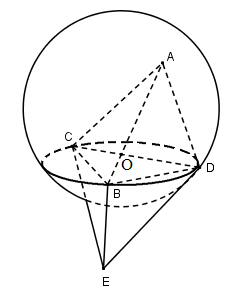
Cho tứ diện \(ABCD\) nội tiếp mặt cầu \((S)\). Lấy một điểm \(E\) nằm khác phía với \(A\) đối với mp \((BCD)\) sao cho \(E\) không nằm trên \((S)\). Xét hình đa diện \(ABCDE\) có sáu mặt là các tam giác \(ABC, ABD, ADC, EBC, ECD, EDB\). Các mặt đó đều nội tiếp đường tròn nhưng hình đa diện \(ABCDE\) không nội tiếp mặt cầu.

Thật vậy nếu có mặt cầu đi qua các đỉnh \(A, B, C, D, E\) thì nó phải đi qua \(A, B, C, D\) nên nó chính là mặt cầu \((S)\), nhưng \(E\) lại không nằm trên \((S)\), vô lí.

Bài 6 trang 45 SGK Hình học 12 Nâng cao

a) Tìm tập hợp các mặt cầu tiếp xúc với ba cạnh của một tam giác cho trước.

b) Chứng minh rằng nếu có mặt cầu tiếp xúc với sáu cạnh của hình tứ diện \(ABCD\) thì \(AB + CD = AC + BD = AD + BC\)

Giải

a)

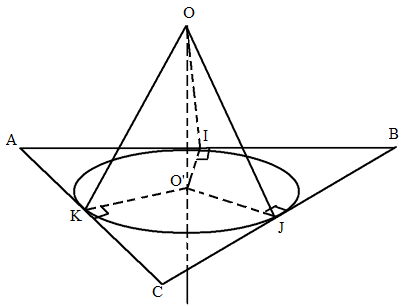
Mặt cầu tâm \(O\) tiếp xúc với ba cạnh \(AB, BC, CA\) của tam giác \(ABC\) lần lượt tại các điểm \(I, J, K\) khi và chỉ khi \(OI \bot AB\,\,,\,\,OJ \bot BC\,\,,\,\,OK \bot CA\)

\(OI = OJ = OK\,\, \in \left( * \right)\)

Gọi \(O’\) là hình chiếu vuông góc của \(O\) trên mp \((ABC)\) thì các điều kiện (*) tương đương với \(O'I \bot AB\,\,,\,\,O'J \bot BC\,\,,\,\,O'K \bot CA\)

\(O'I = O'J = O'K\) hay \(O’\) là tâm đường tròn nội tiếp tam giác \(ABC\).

Từ đó suy ra tập hợp các điểm \(O\) là trục của đường tròn nội tiếp tam giác \(ABC\).

b)

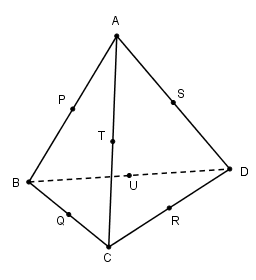
Giả sử mặt cầu \((S)\) nội tiếp với các cạnh \(AB, BC, CD, DA, AC, BD\) lần lượt tại \(P, Q, R, S, T, U\). Ta cần chứng minh: \(AB + CD = AC + BD = AD + BC\)

Theo tính chất của tiếp tuyến ta có:

\(\eqalign{
& AB + CD = AP + PB + CR + RD \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = AT + BU + CT + DU \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {AT + TC} \right) + \left( {BU + UD} \right) = AC + BD \cr} \)

Vậy \(AB + CD = AC + BD\)

Chứng minh tương tự \(AC + BD = AD + BC\)

Vậy \(AB + CD = AC + BD = AD + BC\).

Bài 7 trang 45 SGK Hình học 12 Nâng cao

a) Tính thể tích khối cầu ngoại tiếp hình chóp tam giác đều có cạnh đáy bằng \(a\) và chiều cao bằng \(h\).

b) Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh cùng bằng \(a\). Gọi \(A’, B’, C’, D’\) lần lượt là trung điểm của \(SA, SB, SC, SD\). Chứng minh rằng các điểm \(A, B, C, D, A’, B’, C’, D’\) cùng thuộc một mặt cầu và tính thể tích khối cầu đó.

Giải

a)

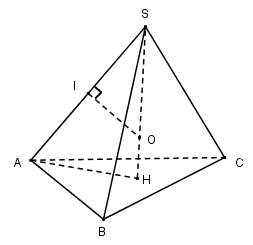
Gọi \(H\) là tâm của tam giác đều \(ABC\). \(SH\) là đường cao của hình chóp đều \(S.ABC\) nên \(SH\) là trục của tam giác \(ABC\).

Trong mặt phẳng \((SAH)\) gọi \(O\) là giao điểm của đường trung trực \(SA\) với \(SH\) thì \(O\) là tâm của mặt cầu ngoại tiếp hình chóp và bán kính của mặt cầu là \(R = SO\).

Gọi \(I\) là trung điểm của \(SA\) thì tứ giác \(AHOI\) nội tiếp nên:

\(SO.SH = SI.SA \Rightarrow SO = {{S{A^2}} \over {2SH}} = {{S{A^2}} \over {2h}}\)

Mà \(S{A^2} = S{H^2} + A{H^2} = {h^2} + {\left( {{{a\sqrt 3 } \over 3}} \right)^2} = {{{a^2} + 3{h^2}} \over 3}\)

Từ đó suy ra \(R = SO = {{{a^2} + 3{h^2}} \over {6h}}\)

Vậy thể tích khối cầu cần tìm là \(V = {{\pi {{\left( {{a^2} + 3{h^2}} \right)}^3}} \over {162{h^3}}}\)

b)

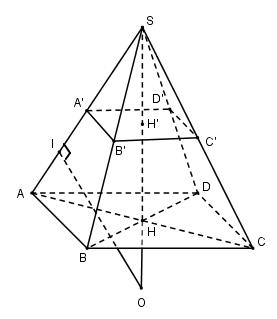
Gọi \(SH\) là đường cao của hình chóp đều \(S.ABCD\) thì \(H\) là tâm của hình vuông \(ABCD\) và \(SH\) đi qua tâm \(H’\) của hình vuông \(A’B’C’D’\).

Mọi điểm nằm trên \(SH\) đều cách đều bốn điểm \(A’, B’, C’, D’\). Trên đường thẳng \(SH\), ta xác định điểm \(O\) sao cho \(OA = OA’\) thì \(O\) cách đều tám điểm \(A, B, C, D, A’, B’, C’, D’\) tức là tám điểm đó nằm trên mặt cầu tâm \(O\), bán kính \(R = OA\). Điểm \(O\) là giao điểm của đường thẳng \(SH\) và mặt phẳng trung trực của đoạn thẳng \(AA’\).

Ta có: \(2{a^2} = A{C^2} = S{A^2} + S{C^2}\) nên tam giác vuông cân tại S suy ra \(\widehat {ASO} = {45^0}\) do đó ASIO vuông cân tại I và \(IS = IO = {{3a} \over 4}\).

Từ đó suy ra \(R = OA = \sqrt {O{I^2} + I{A^2}}  = \sqrt {{{9{a^2}} \over {16}} + {{{a^2}} \over {16}}}  = {{a\sqrt {10} } \over 4}\)

Vậy thể tích khối cầu cần tìm là: \(V = {4 \over 3}\pi {\left( {{{a\sqrt {10} } \over 4}} \right)^3} = {{5\pi {a^3}\sqrt {10} } \over {24}}\)

Giaibaitap.me