Bài 12 trang 82 SGK Hình học 12 Nâng cao

Cho hình chóp S.ABC có đường cao SA = h, đáy là tam giác ABC vuông tại C, AC = b, BC = a. Gọi M là trung điểm của AC và N  là điểm sao cho \(\overrightarrow {SN}  = {1 \over 3}\overrightarrow {SB} \).

a) Tính độ dài đoạn thẳng MN.

b) Tìm sự liên hệ giữa a, b, h để MN vuông góc với SB.

Giải

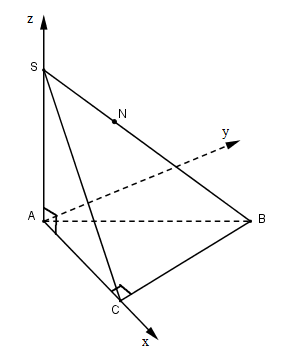
Chọn hệ trục Oxyz như hình vẽ, B nằm trong góc xOy.
Ta có: \(A = \left( {0;0;0} \right),C = \left( {b;0;0} \right),B = \left( {b;a;0} \right),\)

\(S = \left( {0;0;h} \right)\) .

\(M\left( {{b \over 2};0;0} \right),\overrightarrow {SB}  = \left( {b;a; - h} \right)\)

Gọi \(N\left( {x;y;z} \right)\) thì \(\overrightarrow {SN}  = \left( {x;y;z - h} \right)\).

\(\overrightarrow {SN} = {1 \over 3}\overrightarrow {SB} \Leftrightarrow \left\{ \matrix{
x = {b \over 3} \hfill \cr
y = {a \over 3} \hfill \cr
z - h = {{ - h} \over 3} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = {b \over 3} \hfill \cr
y = {a \over 3} \hfill \cr
z = {{2h} \over 3} \hfill \cr} \right.\)

\(\Rightarrow N\left( {{b \over 3};{a \over 3};{{2h} \over 3}} \right)\)

a) 

\(\eqalign{
& \overrightarrow {MN} = \left( {{b \over 3} - {b \over 2};{a \over 3};{{2h} \over 3}} \right) = \left( { - {b \over 6};{a \over 3};{{2h} \over 3}} \right) \cr
& MN = \sqrt {{{{b^2}} \over {36}} + {{{a^2}} \over 9} + {{4{h^2}} \over 9}} \cr&= {1 \over 6}\sqrt {{b^2} + 4{a^2} + 16{h^2}} \cr} \)

b) \(MN \bot SB \Leftrightarrow \overrightarrow {MN} .\overrightarrow {SB}  = 0 \)

\(\Leftrightarrow  - {{{b^2}} \over 6} + {{{a^2}} \over 3} + {{ - 2{h^2}} \over 3} = 0 \Leftrightarrow 4{h^2} = 2{a^2} - {b^2}\)

Bài 13 trang 82 SGK Hình học 12 Nâng cao

Tìm toạ độ tâm và tính bán kính của mỗi mặt cầu sau đây :

a) \({x^2} + {y^2} + {z^2} - 8x + 2y + 1 = 0\)

b) \(3{x^2} + 3{y^2} + 3{z^2} + 6x - 3y + 15z - 2 = 0\)

c) \(9{x^2} + 9{y^2} + 9{z^2} - 6x + 18y + 1 = 0\)

Giải

a) Ta có

\(\eqalign{
& {x^2} + {y^2} + {z^2} - 8x + 2y + 1 = 0 \cr
& \Leftrightarrow \left( {{x^2} - 8x + 16} \right) + \left( {{y^2} + 2y + 1} \right) + {z^2} = 16 \cr
& \Leftrightarrow {\left( {x - 4} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 16 \cr} \)

Mặt cầu có tâm \(I\left( {4; - 1;0} \right)\) và có bán kính R = 4.

b) Ta có

\(\eqalign{
& 3{x^2} + 3{y^2} + 3{z^2} + 6x - 3y + 15z - 2 = 0 \cr
& \Leftrightarrow {x^2} + {y^2} + {z^2} + 2x - y + 5z - {2 \over 3} = 0 \cr
& \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - {1 \over 2}} \right)^2} + {\left( {z + {5 \over 2}} \right)^2} = {{49} \over 6} \cr} \)

Mặt cầu có tâm \(I\left( { - 1;{1 \over 2}; - {5 \over 2}} \right)\) và có bán kính \(R = {{7\sqrt 6 } \over 6}\).

c) 

\(\eqalign{
& 9{x^2} + 9{y^2} + 9{z^2} - 6x + 18y + 1 = 0 \cr
& \Leftrightarrow {x^2} + {y^2} + {z^2} - {2 \over 3}x + 2y + {1 \over 9} = 0 \cr
& \Leftrightarrow {\left( {x - {1 \over 3}} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 1 \cr} \)

Mặt cầu có tâm \(I\left( {{1 \over 3}; - 1;0} \right)\) và có bán kính R = 1.

Bài 14 trang 82 SGK Hình học 12 Nâng cao

Trong mỗi trường hợp sau, hãy viết phương trình mặt cầu :

a) Đi qua ba điểm A(0 ; 8 ; 0), B(4; 6 ; 2), C(0 ; 12 ; 4) và có tâm nằm trên mp(Oyz);

b) Có bán kính bằng 2, tiếp xúc với mặt phẳng (Oyz) và có tâm nằm trên tia Ox;

c) Có tâm I(1 ; 2 ; 3) và tiếp xúc với mp(Oyz). 

Giải

a) Tâm I của mặt cầu nằm trên mp(Oyz) nên \(I\left( {0;b;c} \right)\). Ta tìm b và c để IA = IB = IC. Ta có:

\(\left\{ \matrix{
I{A^2} = I{B^2} \hfill \cr
I{A^2} = I{C^2} \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{
{\left( {8 - b} \right)^2} + {c^2} = {4^2} + {\left( {6 - b} \right)^2} + {\left( {2 - c} \right)^2} \hfill \cr
{\left( {8 - b} \right)^2} + {c^2} = {\left( {12 - b} \right)^2} + {\left( {4 - c} \right)^2} \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{
b = 7 \hfill \cr
c = 5 \hfill \cr} \right.\)

Vậy tâm \(I\left( {0;7;5} \right)\) bán kính

R = IA =\(\sqrt {0 + 1 + 25}  = \sqrt {26} \).

Mặt cầu có phương trình \({x^2} + {\left( {y - 7} \right)^2} + {\left( {z - 5} \right)^2} = 26\).

b) Vì tâm của mặt cầu nằm trên tia Ox và mặt cầu tiếp xúc với mp(Oyz) nên điểm tiếp xúc phải là O, do đó bán kính mặt cầu là R = IO = 2 và \(I\left( {2;0;0} \right)\).

Mặt cầu có phương trình \({\left( {x - 2} \right)^2} + {y^2} + {z^2} = 4\)

c) Vì mặt cầu có tâm \(I\left( {1;2;3} \right)\) và tiếp xúc với mp(Oyz), vậy R = 1. Mặt cầu có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 1\)

Giaibaitap.me