Bài 2.41 trang 102 Sách bài tập (SBT) Toán Hình học 10

Cho tứ giác ABC biết \(a = 7cm,b = 23cm,\widehat C = {130^0}\). Tính \(c,\widehat A,\widehat B\)

Gợi ý làm bài

Theo định lí cô sin ta có:

\(\eqalign{
& {c^2} = {a^2} + {b^2} - 2ab\cos C \cr
& = {7^2} + {23^2} - 2.7.23.\cos {130^0} \approx 785 \cr} \)

\(=  > c \approx 28(cm)\). Theo định lí sin ta có:

\(\eqalign{
& {a \over {\sin A}} = {c \over {\sin C}} \cr
& = > \sin A = {{a{\mathop{\rm sinC}\nolimits} } \over c} \cr
& = {{7.\sin {{130}^0}} \over {28}} \approx 0,1915 \cr} \)

Vậy \(\widehat A \approx {11^0}2'\)

\(\eqalign{
& \widehat B = {180^0} - (\widehat A + \widehat C) \cr
& \approx {180^0} - ({11^0}2' + {130^0}) = {38^0}58' \cr} \)

Bài 2.42 trang 102 Sách bài tập (SBT) Toán Hình học 10

Cho tứ giác ABC biết a = 14cm, b = 18cm, c = 20cm. Tính \(\widehat A,\widehat B,\widehat C\)

Gợi ý làm bài

Theo định lí cô sin ta có:

\(\eqalign{
& {\mathop{\rm cosA}\nolimits} = {{{b^2} + {c^2} - {a^2}} \over {2bc}} \cr
& = {{{{18}^2} + {{20}^2} - {{14}^2}} \over {2.18.20}} = {{528} \over {720}} \approx 0,7333 \cr} \)

Vậy \(\widehat A \approx {42^0}50'\)

\(\eqalign{
& \cos B = {{{a^2} + {c^2} - {b^2}} \over {2ac}} \cr
& = {{{{14}^2} + {{20}^2} - {{18}^2}} \over {2.14.20}} = {{272} \over {560}} \approx 0,4857 \cr} \)

Vậy \(\widehat B \approx {60^0}56'\)

\(\eqalign{
& \widehat C = {180^0} - (\widehat A + \widehat B) \cr
& \approx ({180^0} - ({42^0}50' + {60^0}56') = {76^0}14' \cr} \)

Bài 2.43 trang 103 Sách bài tập (SBT) Toán Hình học 10

Giả sử chúng ta cần đo chiều cao CD của một cái tháp với C là chân tháp, D là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm A, B có khoảng cách AB = 30 m sao cho ba điểm A, B, C thẳng hàng người ta đo được các góc \(\widehat {CAD} = {43^0},\widehat {CBD} = {67^0}\) (h.2.18). Hãy tính chiều cao CD của tháp

Gợi ý làm bài

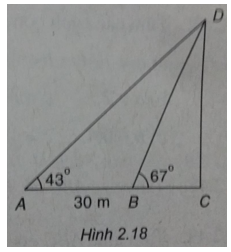
Muốn tính chiều cao CD của tháp, trước hết ta hãy tính góc \(\widehat {ADB}\)

\(\widehat {ADB} = {67^0} - {43^0} = {24^0}\)

Theo định lí sin đối với tam giác ABD ta có:

\(\eqalign{
& {{BD} \over {\sin {{43}^0}}} = {{AB} \over {\sin {{24}^0}}} \cr
& = > BD = {{30.\sin {{43}^0}} \over {\sin {{24}^0}}} \approx 50,30(m) \cr} \)

Trong tam giác vuông BCD ta có:

\(\eqalign{
& \sin {67^0} = {{CD} \over {BD}} \cr
& = > CD = BD.\sin {67^0} \approx 50,30.\sin {67^0} \cr} \)

Hay \(CD \approx 46,30(m)\)

Bài 2.44 trang 103 Sách bài tập (SBT) Toán Hình học 10

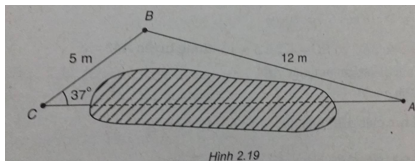
Khoảng cách từ A đến C không thể đo trực tiếp vì phải qua một đầm lầy nên người ta làm như sau:  Xác định một điểm B có khoảng cách AB = 12m và đo được góc \(\widehat {ACB} = {37^0}\) (H.2.19). Hãy tính khoảng cách AC biết rằng BC = 5 m.

Gợi ý làm bài

Theo định lí sin đối với tam giác ABC ta có:

\({{BC} \over {{\mathop{\rm sinA}\nolimits} }} = {{AB} \over {{\mathop{\rm sinC}\nolimits} }} \Leftrightarrow {5 \over {\sin A}} = {{12} \over {\sin {{37}^0}}}\)

\( =  > \,\sin A = {{5.\sin {{37}^0}} \over {12}} \approx 0,2508\)

\( =  > \widehat A \approx {14^0}31'\)

\(\widehat B \approx ({180^0} - ({37^0} + {14^0}31') = {128^0}29'\)

\(\eqalign{
& {{AC} \over {\sin B}} = {{12} \over {{\mathop{\rm sinC}\nolimits} }} \cr
& = > AC = {{12\sin B} \over {\sin C}} \approx {{12.\sin {{128}^0}29'} \over {\sin {{37}^0}}} \approx 15,61(m) \cr} \)

Vậy khoảng cách \(AC \approx 15,61(m)\)

Giaibaitap.me