Bài 13 trang 222 SGK Đại số 10 Nâng cao

Chứng minh rằng:

a) ${{{a^2} + 6} \over {\sqrt {{a^2} + 2} }} \ge 4\,\,\,\,(a \in R)$

b) ${{{a^2}} \over {{b^2}}} + {{{b^2}} \over {{c^2}}} + {{{c^2}} \over {{a^2}}} \ge {a \over c} + {c \over b} + {b \over a}\,\,\,(a,\,b,\,c\, \in R)$

Đáp án

a) Áp dụng bất đẳng thức Cô-si, ta có:

${{{a^2} + 6} \over {\sqrt {{a^2} + 2} }} = {{({a^2} + 2) + 4} \over {\sqrt {{a^2} + 2} }} = \sqrt {{a^2} + 2}  + {4 \over {\sqrt {{a^2} + 2} }} \ge$

$2\sqrt {\sqrt {{a^2} + 2} .{4 \over {\sqrt {{a^2} + 2} }}}  = 4$ 

b) Ta có:

 ${{{a^2}} \over {{b^2}}} + {{{b^2}} \over {{c^2}}} \ge 2\sqrt {{{{a^2}} \over {{b^2}}}.{{{b^2}} \over {{c^2}}}}  = 2|{a \over c}|\, \ge {{2a} \over c}$

Tương tự ta có:

$\left\{ \matrix{ {{{b^2}} \over {{c^2}}} + {{{c^2}} \over {{a^2}}} \ge 2{b \over a} \hfill \cr {{{c^2}} \over {{a^2}}} + {{{a^2}} \over {{b^2}}} \ge 2{c \over b} \hfill \cr} \right.$

Từ đó suy ra: $2({{{a^2}} \over {{b^2}}} + {{{b^2}} \over {{c^2}}} + {{{c^2}} \over {{a^2}}}) \ge 2({a \over c} + {c \over b} + {b \over a})$

Bài 14 trang 222 SGK Đại số 10 Nâng cao

Tìm giá trị nhỏ nhất của các hàm số sau

a) $f(x) = x + {2 \over {x + 2}}$ trên khoảng $(-2; +∞)$

b) $g(x) = 3{x^2} + {1 \over x}$ trên khoảng $(0; +∞)$

Đáp án

a) Áp dụng bất đẳg thức Cô-si, ta có:

$f(x) = x + 2{2 \over {x + 2}} - 2 \ge 2\sqrt {(x + 2){2 \over {x + 2}}}  - 2$

                                                                     $= 2\sqrt 2  - 2$ 

Dấu “=”xảy ra khi và chỉ khi:

$x + 2 = {2 \over {x + 2}} \Leftrightarrow {(x + 2)^2} = 2 \Leftrightarrow \left\{ \matrix{ x = \sqrt 2 - 2 \hfill \cr x = - \sqrt 2 - 2 \hfill \cr} \right.$

b) Áp dụng bất đẳng thức Cô-si cho ba số, ta có:

$g(x) = 3{x^2} + {1 \over {2x}} + {1 \over {2x}} \ge 3\root 3 \of {3{x^2}.{1 \over {2x}}.{1 \over {2x}}}  = 3\root 3 \of {{3 \over 4}}$

Dấu “=” xảy ra $\Leftrightarrow 3{x^2} = {1 \over {2x}} \Leftrightarrow x = \root 3 \of {{1 \over 6}}$

Vậy: $\min \,g(x) = 3\root 3 \of {{3 \over 4}}  \Leftrightarrow x = \root 3 \of {{1 \over 6}}$

Bài 15 trang 222 SGK Đại số 10 Nâng cao

Tìm giá trị lớn nhất của hàm số: $f(x) = (2 - x)(2x + 1)$ trên $(-0,5; 2)$

Đáp án

Áp dụng bất đẳng thức Cô-si, ta có:

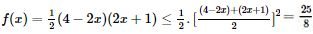
Dấu “=” xảy ra khi $\Leftrightarrow 4 - 2x = 2x + 1 \Leftrightarrow x = {3 \over 4}$

Vậy $\max \,f(x) = {{25} \over 8} \Leftrightarrow x = {3 \over 4}$

Bài 16 trang 222 SGK Đại số 10 Nâng cao

Giải các hệ bất phương trình

a)

$\left\{ \matrix{ {x^2} - 4 > 0 \hfill \cr {1 \over {x + 1}} + {1 \over {x + 2}} \ge {1 \over x} \hfill \cr} \right.$

b) 

$\left\{ \matrix{ {x^2} + 3x + 2 < 0 \hfill \cr {x \over {x + 1}} \ge 0 \hfill \cr} \right.$

Đáp án

a) Ta giải từng bất phương trình trong hệ đã cho:

${x^2} - 4 > 0 \Leftrightarrow \left[ \matrix{ x < - 2 \hfill \cr x > 2 \hfill \cr} \right.$

Tập nghiệm là S₁= $(-∞; -2) ∪ (2, +∞)$

$\eqalign{ & {1 \over {x + 1}} + {1 \over {x + 2}} \ge {1 \over x}\cr& \Leftrightarrow {{x(x + 2) + x(x + 1) - (x + 1)(x - 2)} \over {x(x + 1)(x + 2)}} \ge 0 \cr & \Leftrightarrow {{{x^2} - 2} \over {x(x + 1)(x + 2)}} \ge 0 \cr}$

Lập bảng xét dấu:

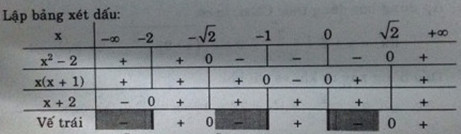
Vậy ${S_2} = ( - 2; - \sqrt 2 {\rm{]}}\, \cup \,( - 1,0)\, \cup \,{\rm{[}}\sqrt 2 , + \infty )$

Từ đó tập nghiệm của hệ bất phương trình là: S = S₁ ∩ S₂ = $(2, +∞)$

b) Ta có:

$\left\{ \matrix{ {x^2} + 3x + 2 < 0 \hfill \cr {x \over {x + 1}} \ge 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ - 2 < x < - 1 \hfill \cr \left[ \matrix{ x < - 1 \hfill \cr x \ge 0 \hfill \cr} \right. \hfill \cr} \right.$

$\Leftrightarrow - 2 < x < 1$ 

Vậy $S = (-2, -1)$

Giaibaitap.me