Bài 12 trang 52 SGK Hình học 10 nâng cao

Bài 12. Cho đoạn thẳng \(AB\) cố định, \(AB = 2a\) và một số \({k^2}\). Tìm tập hợp các điểm \(M\) sao cho \(M{A^2} - M{B^2} = {k^2}\).

Hướng dẫn trả lời

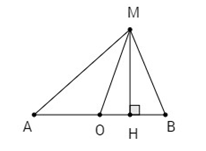
Gọi \(O\) là trung điểm đoạn \(AB, H\) là hình chiếu của \(M\) lên \(AB\). Ta có

\(\eqalign{
& M{A^2} - M{B^2} = {k^2}\,\,\, \Leftrightarrow \,\,{\overrightarrow {MA} ^2} - {\overrightarrow {MB} ^2} = {k^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow (\overrightarrow {MA} + \overrightarrow {MB} ).\,(\overrightarrow {MA} - \overrightarrow {MB} ) = {k^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 2\overrightarrow {MO} .\,\overrightarrow {BA} = {k^2}\, \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 2\left( {\overrightarrow {MH} + \overrightarrow {HO} } \right).\overrightarrow {BA} \cr
& .\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 2\overrightarrow {HO} .\,\overrightarrow {BA} = {k^2} \cr} \)

( Vì \(\overrightarrow {MH} .\overrightarrow {BA}  = \overrightarrow 0 \))

Suy ra \(H\) cố định nằm trên tia \(OB\) và \(OH = {{{k^2}} \over {4a}}\).

 Do \(H\) là hình chiếu của \(M\) lên \(AB\) nên tập hợp các điểm \(M\) là đường thẳng vuông góc với \(AB\) tại \(H, H\) nằm trên tia  \(OB\) sao cho \(OH = {{{k^2}} \over {4a}}\).

Bài 13 trang 52 SGK Hình học 10 nâng cao

Bài 13. Trong mặt phẳng tọa độ, cho \(\overrightarrow u  = {1 \over 2}\overrightarrow i  - 5\overrightarrow j \) và \(\overrightarrow v  = k\overrightarrow i  - 4\overrightarrow j \).

a) Tìm các giá trị của \(k\) để \(\overrightarrow u  \bot \overrightarrow v \);

b) Tìm các giá trị của \(k\) để \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow v } \right|\).

Hướng dẫn trả lời

Ta có \(\overrightarrow u  = ({1 \over 2}\,;\, - 5)\,;\,\,\,\overrightarrow v  = (k\,;\, - 4)\,\).

a) \(\overrightarrow u  \bot \overrightarrow v \,\, \Leftrightarrow \,\,\overrightarrow u .\,\overrightarrow v  = 0\,\, \Leftrightarrow \,\,{1 \over 2}.k + ( - 5).( - 4) = 0\,\, \Leftrightarrow \,\,k =  - 40.\)

b) \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow v } \right|\,\, \Leftrightarrow \,\,\sqrt {{1 \over 4} + 25}  = \sqrt {{k^2} + 16} \,\, \Leftrightarrow \,\,{{101} \over 4} = {k^2} + 16\,\, \Leftrightarrow \,\,k =  \pm {{\sqrt {37} } \over 2}\)

Bài 14 trang 52 SGK Hình học 10 nâng cao

Bài 14. Trong mặt phẳng tọa độ, cho tam giác \(ABC\) có các đỉnh \(A( - 4\,;\,1),\,B(2\,;\,4),\,C(2\,;\, - 2)\).

a) Tính chu vi và diện tích của tam giác đó.

b) Tìm tọa độ của trọng tâm \(G\), trực tâm \(H\) và tâm \(I\) của đường tròn ngoại tiếp tam giác \(ABC\). Từ đó hãy kiểm tra tính chất thẳng hàng của ba điểm \(I, G, H\).

Hướng dẫn trả lời

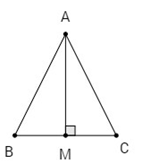
a) Ta có \(\overrightarrow {AB}  = (6\,;\,3)\,,\,\,\overrightarrow {AC}  = (6\,;\, - 3)\,,\,\,\overrightarrow {BC}  = (0\,;\, - 6).\) Suy ra 

\(\eqalign{
& AB = \sqrt {{6^2} + {3^2}} = \sqrt {45} = 3\sqrt 5 \cr
& AC = \sqrt {{6^2} + {{( - 3)}^2}} = \sqrt {45} = 3\sqrt 5 \cr
& BC = \sqrt {{0^2} + {{( - 6)}^2}} = \sqrt {36} = 6 \cr} \)

Tam giác \(ABC\) cân tại \(A\).

Chu vi tam giác \(ABC\) là \(3\sqrt 5  + 3\sqrt 5  + 6 = 6\sqrt 5  + 6\).

Gọi \(M\) là trung điểm của \(BC\) thì \(AM\) là đường cao của ta giác \(ABC\).

Ta có \(M(2\,;\,1)\,,\,\,\overrightarrow {AM}  = (6\,;\,0)\,\, \Rightarrow \,\,AM = \sqrt {{6^2} + 0}  = 6\).

Diện tích tam giác \(ABC\) là

 \({S_{ABC}} = {1 \over 2}BC.AM = {1 \over 2}.6.6 = 18\)

b)  Tọa độ trọng tâm \(G\) của tam giác \(ABC\) là

\(\left\{ \matrix{
{x_G} = {1 \over 3}({x_A} + {x_B} + {x_C}) = {1 \over 3}( - 4 + 2 + 2) = 0 \hfill \cr
{y_G} = {1 \over 3}({y_A} + {y_B} + {y_C}) = {1 \over 3}(1 + 4 - 2) = 1 \hfill \cr} \right.\,\)

Vậy \(G\,(0\,;\,1)\).

Gọi \(H\,({x_H}\,,\,{y_H})\) là trực tâm tam giác \(ABC\). Ta có

\(\eqalign{
& \left\{ \matrix{
\overrightarrow {AH} .\,\overrightarrow {BC} = 0 \hfill \cr
\overrightarrow {BH} .\,\overrightarrow {AC} = 0 \hfill \cr} \right.\,\, \Leftrightarrow \,\,\left\{ \matrix{
({x_H} + 4).0 + ({y_H} - 1).( - 6) = 0 \hfill \cr
({x_H} - 2).6 + ({y_H} - 4).( - 3) = 0 \hfill \cr} \right.\,\, \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,\left\{ \matrix{
{x_H} = {1 \over 2}\hfill \cr
{y_H} = 1 \hfill \cr} \right. \cr} \)

Vậy \(H\,\left( {{1 \over 2}\,;\,1} \right)\).

Gọi \(I\,({x_I}\,,\,{y_I})\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Ta có

\(\eqalign{
& \left\{ \matrix{
A{I^2} = B{I^2} \hfill \cr
A{I^2} = C{I^2} \hfill \cr} \right.\,\, \Leftrightarrow \,\,\left\{ \matrix{
{({x_I} + 4)^2} + {({y_I} - 1)^2} = {({x_I} - 2)^2} + {({y_I} - 4)^2} \hfill \cr
{({x_I} + 4)^2} + {({y_I} - 1)^2} = {({x_I} - 2)^2} + {({y_I} + 2)^2} \hfill \cr} \right. \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,\left\{ \matrix{
{x_I}^2 + 8{x_I} + 16 + {y_I}^2 - 2{y_I} + 1 = {x_I}^2 - 4{x_I} + 4 + {y_I}^2 - 8{y_I} + 16 \hfill \cr
{x_I}^2 + 8{x_I} + 16 + {y_I}^2 - 2{y_I} + 1 = {x_I}^2 - 4{x_I} + 4 + {y_I}^2 + 4{y_I} + 4 \hfill \cr} \right. \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,\left\{ \matrix{
4{x_I} + 2{y_I} = 1 \hfill \cr
4{x_I} - 2{y_I} = - 3 \hfill \cr} \right.\,\, \Leftrightarrow \,\,\left\{ \matrix{
{x_I} = - {1 \over 4} \hfill \cr
{y_I} = 1 \hfill \cr} \right. \cr} \)

Vậy \(I\,( - {1 \over 4}\,;\,1)\).

Khi đó, ta có \(\overrightarrow {IG}  = \left( {{1 \over 4}\,;\,0} \right)\,,\,\,\,\overrightarrow {IH}  = \left( {{3 \over 4}\,;\,0} \right)\).

Do đó \(\overrightarrow {IG}  = {1 \over 3}\overrightarrow {IH} \)  ,

Suy ra \(I, G, H\) thẳng hàng.

Giaibaitap.me