Bài 15 trang 64 SGK Hình học 10 nâng cao
Bài 15. Tam giác \(ABC\) có \(a = 12, b = 13, c = 15\). Tính \(\cos A\) và góc \(A\).
Hướng dẫn trả lời
Áp dụng công thức tính ta có
\(\eqalign{
& \cos A = {{{b^2} + {c^2} - {a^2}} \over {2bc}} = {{{{13}^2} + {{15}^2} - {{12}^2}} \over {2.13.15}} = {{25} \over {39}} \cr
& \Rightarrow \,\,\widehat A \approx {50^0} \cr} \)
Bài 16 trang 64 SGK Hình học 10 nâng cao
Bài 16. Cho tam giác \(ABC\) có \(AB = 5,\,AC = 8,\,\widehat A = {60^0}\). Kết quả nào trong các kết quả sau là độ dài cạnh \(BC\) ?
a) \(\sqrt {129} \); b) \(7\);
c) \(49\); d) \(\sqrt {69} \).
Hướng dẫn trả lời
Ta có \(B{C^2} = {a^2} = {b^2} + {c^2} - 2bc.\cos A = {8^2} + {5^2} - 2.8.5.\cos {60^0} = 49\)
\( \Rightarrow \,\,BC = 7\).
Chọn b).
Bài 17 trang 65 SGK Hình học 10 nâng cao
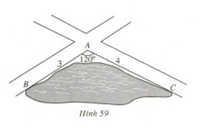
Bài 17. Hình 59 vẽ một hồ nước nằm ở góc tạo bởi hai con đường. Bốn bạn An, Cường , Trí, Đức dự đoán khoảng cách từ B đến C như sau
An : \(5 km\)
Cường : \(6 km\)
Trí : \(7 km\)
Đức : \(5,5 km\).
Biết rằng khoảng cách từ \(A\) đến \(B\) là \(3 km\), khoảng cách từ \(A\) đến \(C\) là \(4 km\), góc \(BAC\) là \({120^0}\).
Hỏi dự đoán của bạn nào sát với thực tế nhất ?
Hướng dẫn trả lời
Áp dụng định lí cosin ta có
\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC} = {3^2} + {4^2} - 2.3.4.\cos {120^0} \cr
& \,\,\,\,\,\,\,\,\,\,\,\;\ = 9 + 16 + 12 = 37 \cr
& \Rightarrow BC = \sqrt {37} \approx 6,1 \cr} \)
Vậy bạn Cường dự đoán sát với thực tế nhất.
Bài 18 trang 65 SGK Hình học 10 nâng cao
Bài 18. Cho tam giác \(ABC\). Chứng minh các khẳng định sau
a) Góc \(A\) nhọn khi và chỉ khi \({a^2} < {b^2} + {c^2}\);
a) Góc \(A\) tù khi và chỉ khi \({a^2} > {b^2} + {c^2}\);
a) Góc \(A\) vuông khi và chỉ khi \({a^2} = {b^2} + {c^2}\).
Hướng dẫn trả lời
Ta có \(\cos A = {{{b^2} + {c^2} - {a^2}} \over {2bc}}\)
a) \(A\) nhọn \( \Leftrightarrow \,\,\cos A > 0\,\, \Leftrightarrow \,\,{b^2} + {c^2} > {a^2}\).
b) \(A\) tù \( \Leftrightarrow \,\,\cos A < 0\,\, \Leftrightarrow \,\,{b^2} + {c^2} < {a^2}\) .
c) \(A\) vuông \( \Leftrightarrow \,\,\cos A = 0\,\, \Leftrightarrow \,\,{b^2} + {c^2} = {a^2}\) .
Giaibaitap.me
Giải bài tập trang 65 bài 3 hệ thức lượng trong tam giác SGK Hình học 10 nâng cao. Câu 19: Tính...
Giải bài tập trang 65, 66 bài 3 hệ thức lượng trong tam giác SGK Hình học 10 nâng cao. Câu 23: Chứng minh rằng bán kính các đường tròn ngoại tiếp các tam giác ...
Giải bài tập trang 66 bài 3 hệ thức lượng trong tam giác SGK Hình học 10 nâng cao. Câu 27: Chứng minh rằng trong một hình bình hành, tổng bình phương các cạnh bằng tổng bình phương của hai đường chéo...
Giải bài tập trang 66 bài 3 hệ thức lượng trong tam giác SGK Hình học 10 nâng cao. Câu 31: Chứng minh rằng...
