Bài 1.1 trang 12 Sách bài tập (SBT) Toán Hình học 10
Hãy tính số các vec tơ (khác \(\overrightarrow 0 \)) mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho trong các trường hợp sau:
a) Hai điểm
b) Ba điểm;
c) Bốn điểm.
Gợi ý làm bài
a)Với hai điểm A, B có hai vec tơ \(\overrightarrow {AB} ,\overrightarrow {BA} \)
b)Với ba điểm A, B, C có 6 vec tơ \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {BC} ,\overrightarrow {CB} \)
c)Với bốn điểm A, B, C, D có 12 véc tơ (học sinh tự liệt kê).
Bài 1.2 trang 12 Sách bài tập (SBT) Toán Hình học 10
Cho hình vuông ABCD có tâm O. Liệt kê tất cả các vec tơ bằng nhau (khác \(\overrightarrow 0 \)) nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.
Gợi ý làm bài
(h 1.34)
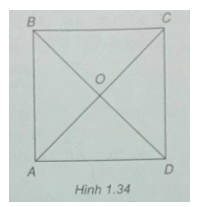
\(\overrightarrow {BC} = \overrightarrow {AD} ,\overrightarrow {CB} = \overrightarrow {DA} \)
\(\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {BA} = \overrightarrow {CD} \)
\(\overrightarrow {OB} = \overrightarrow {DO} ,\overrightarrow {BO} = \overrightarrow {OD} \)
\(\overrightarrow {AO} = \overrightarrow {OC} ,\overrightarrow {CO} = \overrightarrow {OA} \)
Bài 1.3 trang 12 Sách bài tập (SBT) Toán Hình học 10
Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh \(\overrightarrow {NP} = \overrightarrow {MQ} \) và \(\overrightarrow {PQ} = \overrightarrow {NM} \)
Gợi ý làm bài
(h. 1.35)
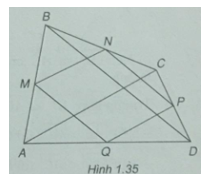
MN = PQ và MN // PQ
Vì chúng đều bằng \({1 \over 2}\) AC và đều song song với AC .
Vậy tứ giác MNPQ là hình bình hành nên ta có:
\(\overrightarrow {NP} = \overrightarrow {MQ} ,\overrightarrow {PQ} = \overrightarrow {NM} \)
Bài 1.4 trang 12 Sách bài tập (SBT) Toán Hình học 10
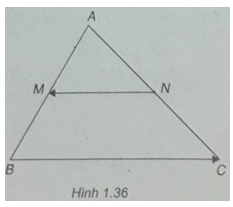
Cho tam giác ABC. Các điểm M và N lần lượt là trung điểm của các cạnh AB và AC. So sánh độ dài của hai vec tơ \(\overrightarrow {NM} \) và \(\overrightarrow {BC} \). Vì sao có thể nói hai vec tơ này cùng phương?
Gợi ý làm bài
(h. 1. 36)
MN // BC và \(MN = {1 \over 2}BC\) hay \(\left| {\overrightarrow {MN} } \right| = {1 \over 2}\left| {\overrightarrow {BC} } \right|\)
Vì MN // BC nên \(\overrightarrow {NM} \) và \(\overrightarrow {BC} \) cùng phương.
Giaibaitap.me
Giải bài tập trang 12 bài 1 các định nghĩa Sách bài tập (SBT) Toán Hình học 10. Câu 1.5: Cho tứ giác ABCD, chứng minh rằng...
Giải bài tập trang 23 bài 2 tổng và hiệu của hai vecto Sách bài tập (SBT) Toán Hình học 10. Câu 1.8: Cho năm điểm A, B, C, D và E. Hãy xác định tổng ...
Giải bài tập trang 23 bài 2 tổng và hiệu của hai vecto Sách bài tập (SBT) Toán Hình học 10. Câu 1.12: Gọi O là giao điểm hai đường chéo của hình bình hành ABCD...
Giải bài tập trang 23 bài 2 tổng và hiệu của hai vecto Sách bài tập (SBT) Toán Hình học 10. Câu 1.16: Cho ngũ giác ABCDE. Chứng minh...
