Bài 1 trang 190 SGK Đại số 10 Nâng cao
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Số đo của cung trong phụ thuộc vào bán kính của nó
b) Độ dài của cung tròn tỉ lệ với số đo của cung tròn
c) Độ dài của cung tròn tỉ lệ với bán kính của nó
d) Nếu Ou, Ov là hai tia đối nhau thì số đo góc lượng giác (Ou; Ov) là (2k + 1)π, k∈Z.
Đáp án
a) Sai
b) Đúng
c) Đúng
d) Đúng
Bài 2 trang 190 SGK Đại số 10 Nâng cao
Kim phút và kim giờ của đồng hồ lớn nhà bưu điện bờ hồ Hà Nội, theo thứ tự dài 1,75 m và 1,26 m. Hỏi trong 15 phút mũi kim phút vạch nên cung tròn có độ dài là bao nhiêu mét? Cũng câu hỏi đó cho mũi kin giờ.
Đáp án
Trong 15 phút, mũi kim phút vạch cung tròn có số đo \({\pi \over 2}\) rad nên cung đó có độ dài là:
\({\pi \over 2}.1,75\, \approx 2,75(m)\)
Mũi kim giờ vạch cung tròn có số đo \({\pi \over {24}}\) rad nên cung đó có độ dài:
\({\pi \over {24}}.1,26 = 0,16\,(m)\)
Bài 3 trang 190 SGK Đại số 10 Nâng cao
Điền vào các ô trống trong bảng
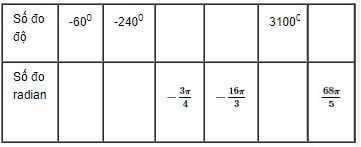
Đáp án
Áp dụng công thức \({\alpha \over \pi } = {a \over {180}}\) (ta được tính bằng độ, α được tính bằng radian)
Ta có bảng sau:

Bài 4 trang 190 SGK Đại số 10 Nâng cao
a) Đổi số đo độ của các cung tròn sau thành số đo radian (chính xác đến phần nghìn):
21o30' và 75o54'.
b) Đổi số đo radian của các cung tròn sau ra số đo độ : 2,5 (rad) và 2/π (rad) (có thể dùng máy tính bỏ túi).
Đáp án
a) Ta có:
\(\eqalign{
& {21^0}30' = {{21,5\pi } \over {180}} \approx 0,375\,\,(rad) \cr
& {75^0}54' = {{75,9\pi } \over {180}} \approx 1,325\,\,(rad) \cr} \)
b) Ta có:
\(\eqalign{
& 2,5\,rad\,\, = \,{({{2,5.180} \over \pi })^0} \approx {143^0}14' \cr
& {2 \over \pi }rad\, = ({{{2 \over \pi }180} \over \pi }) = {({{360} \over \pi })^0} \approx {36^0}29' \cr} \)
Giaibaitap.me
Giải bài tập trang 190, 191 bài 1 góc lượng giác và cung lượng giác SGK Đại số 10 Nâng cao. Câu 5: Coi kim giờ của đồng hồ là tia Ou, kim phút là tia Ov. Hãy tìm số đo của góc lượng giác (Ou;Ov) khi đồng hồ chỉ 3 giờ, chỉ 4 giờ, chỉ 9 giờ , chỉ 10 giờ...
Giải bài tập trang 191 bài 1 góc lượng giác và cung lượng giác SGK Đại số 10 Nâng cao. Câu 8: Cho ngũ giác đều A0A1A2A3A4 nội tiếp đường tròn tâm O...
Giải bài tập trang 191, 192 bài 1 góc lượng giác và cung lượng giác SGK Đại số 10 Nâng cao. Câu 11: Chứng minh rằng...
Giải bài tập trang 199, 200 bài 2 giá trị của góc (cung) lượng giác SGK Đại số 10 Nâng cao. Câu 14: Mỗi khẳng định sau đúng hay sai?...
